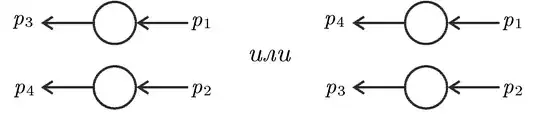The vertex function contains information about:
- The existence of bounded states & their spectrum
- Effective interactions in the theory
- Scattering amplitudes in the theory
To illustrate these statements, let us consider the interaction $U(r_1-r_2,t_1-t_2)$ between two particles and solve the respective Bethe-Salpeter equation. First, consider the interaction $U(r_1-r_2)\delta(t_1-t_2)$, so that the interaction is instantaneous. The equation for the vertex function then is
$$K_{12,34}=(2\pi)^8\delta_{p1p3}\delta_{p_2p_4}G_0^{(1)}(p_1)G_0^{(2)}(p_2)+G_0^{(1)}(p_1)G_0^{(2)}(p_2)G_0^{(1)}(p_3)G_0^{(2)}(p_4)i\Gamma_{p_1p_2p_3p_4}(2\pi)^4\delta_{p_1+p_2,p_3+p_4},$$
where $K_{12,34}$ is the two-particle Green function and upper indices denote particles. Then, you can write down the Bethe-Salpeter equation and extract the irreducible vertex part $\Gamma_0$. In case of instantaneous interaction, $U(\omega,k)=U(k)$. The first order diagram for the irreducible vertex part is zero,
$$\int d\omega G_0^{(1)}(\epsilon_1-\omega)G_0^{(2)}(\epsilon_2-\omega)=0,$$
because poles of both Green functions,
$$\omega_1=\epsilon_1-\frac{p_{1+}^2}{2m}+i\delta,\omega_1=\epsilon_2-\frac{p_{2-}^2}{2m}+i\delta$$
are in the upper half-plane. Then, you can show that all the diagrams with crossing lines go to zero. At second order, the irreducible vertex function is just
$$\Gamma_0(p_1,p_2,p_1+q,p_2-q)=U(q).$$
Then, you can notice that the vertex function does not depend on frequency $\omega$. Therefore, all dependence on frequency comes from the Green functions,
$$i\int\frac{d\omega}{2\pi}G_0^{(1)}(\epsilon_1-\omega)G_0^{(2)}(\epsilon+\omega)=\frac{1}{\epsilon_1+\epsilon_2-p_{1+}^2/2m_1-p_{2-}^2/2m+i0},$$
where $p_{i\pm}=p_i\pm k$. The denominator can be simplified by introducing CM energy and relative motion energy,
$$\frac{p^2}{2m_1}+\frac{(p')^2}{2m_2}=\frac{P^2}{2M}+\frac{p_{\text{rel}}^2}{2\mu},P=p+p',p_{\text{rel}}=\frac{m_2p-m_1p'}{m_1+m_2}.$$
These manipulation give the following form of the Bethe-Salpeter equation,
$$\boxed{\Gamma(k,k')=U(k-k')+\int\frac{d^3q}{(2\pi)^3}\frac{U(k-q)\Gamma(p,k')}{\Omega_0-q^2/(2\mu)+i0},}$$
where $\mu=m_1m_2/(m_1+m_2)$, $\Omega_0=\Omega-P^2/(2m)$, $M=m_1+m_2$, $\Omega=\omega_1+\omega_2=\omega_3+\omega_4$.
So, you see that there is a bounded state with mass $M=2m$ with dispersion law $P^2/(2M)$.
You can consider the structure of the vertex function in a theory with a 4-fermion contact attractive interaction and see that in this theory the vertex function has a pole. The existence of such poles corresponds to the Cooper instability and it signals that one should carefully choose the ground state of theory to develop perturbation theory.
Then, your statement about polarization operator and screening length in plasma relates to the structure of the vertex function, too. As you know, one should sum all the diagrams with 1-loop insertions. You can also see that a bubble is included into the vertex function. The vertex function is
$$\Gamma_{12}(k,\omega_m)=\frac{4\pi e^2Z_1Z_2}{k^2\left[1-\frac{4\pi e^2}{k^2}(\Pi_e(k,\omega_m)+Z^2\Pi_i(k,\omega_m))\right]},$$
where $\Pi_e$ & $\Pi_i$ are polarization operators of electrons and ions. Straightforward calculation yields
$$\Gamma_{12}=\frac{4\pi e^2Z_1Z_2}{k^2+\kappa_i^2},$$
where $\kappa_i$ is the ion screening length.
But you should distinguish between the polarization operator $\Pi$ and the vertex function $\Gamma$. The polarization operator comes from self-energy, which is the one-particle irreducible diagram and the vertex function is related to the two-particle irreducible diagrams. In case of Debye screening in plasma we can consider the renormalization of the "interaction propagator" by bubble series or we can consider 4-fermion process, which describes two-fermion scattering via renormalized (="bubbled" propagator). In other words, you consider propagator renormalization and then say that this renormalized propagator modifies interaction or you can consider interaction renormalization with a vertex function.
In the case of superconductivity:
To emphasize mentioned facts, here are three diagrams (I am lazy to draw them, sorry)

and the entire question is about the singularities of these diagrams. All the singularities comes from the poles of the Green functions in loops. Indeed, to perform integration over energy, you should use an appropriate contour, but external momenta can pinch this contour and the singularity appears. You can show that for the first diagram (from left to right) a singularity appears for $p_1+p_2\approx 0$, for the second and third, $p_2-p_1-k\approx 0$ and $k\approx 0$, respectively. The last diagram defines Fermi liquid theory, whereas the first diagram corresponds to the Cooper instability. The second diagram is "rare".
To conclude, I would like to emphasize:
- the vertex function defines effective interaction in the theory
- vertex function shows the existence of bounded states in theory
The case of vertex functions in condensed matter is more interesting than in QED. For QED, we define the vertex function via a four-point correlator,
$$K_{ik,lm}=\langle T\psi_{i1}\psi_{k2}\bar{\psi}_{l3}\bar{\psi}_{m4}\rangle$$
and can easily consider this correlator in momentum representation. It is worth mentioning that one should also take into account all the loop corrections. From the structure of this correlator, you can extract the reducible part,
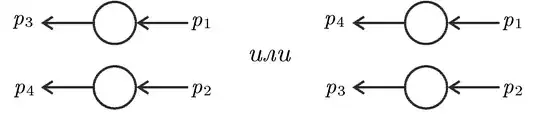
which just gives the exact propagator of two particles without scattering. The last term is more interesting and represents the irreducible part. Finally, you can see that
$$i\mathcal{M}_{fi}=\bar{u}_i(p_3)\bar{u}_k(p_4)\left[-ie\Gamma_{ik,lm}(p_3,p_4;p_1,p_2)\right]u_l(p_1)u_m(p_2),$$
where $i\mathcal{M}_{fi}$ is exactly the scattering amplitude. The next picture is the 4-point correlator for fermions,

and in the non-crossing case (for instance, in superconductivity theory) the vertex function becomes