5

What will happen to a single photon when it goes through a prism?

Will it just be deflected in the direction related to its frequency?

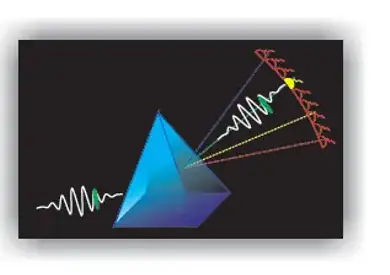
I made this drawing for better understanding, here if I place a set of detectors after the prism, only one of them would detect the photon, contrary to a polychromatic wave light where all of them would trigger. Does this actually happen? enter image description here

Jasper
  • 1,778
E.phy
  • 583

1 Answers1

3

A good answer to this question would require knowing the source of the single photon you're asking about. If the beam from a laser emitting at, say, 532 nm and having a bandwidth of, say, 0.1 nm, is passed through a prism, the angular spread of the beam will be extremely small -- let's say an angle of $\alpha$. Any individual photon in that beam will contain a mix of wavelengths and will land somewhere within the angular spread $\alpha$. If the beam comes from a continuum laser which has a bandwidth that covers the visible spectrum from ~650 nm to ~400nm, then the beam will spread into a rainbow upon passing through the prism, and will cover a much wider angle $\beta$. And, any single photon in the beam will land somewhere within the angular spread $\beta$.

A photon can only be detected once. Before detection, its frequency (and polarization) are indeterminate. That means those properties don't have a value until they are detected/measured. It's not that the properties are not known; the properties don't have a value. The wave packet constituting a photon before detection is just a packet of probability densities, specifying the likelihood that a measurement will yield any particular value. So the wave packet of any photon in the beam is spread by a prism just as the beam is spread, but as soon as the photon is detected somewhere, we assign it a wavelength that it didn't have just before detection. If instead of detecting the photon at that point, we let it pass through a slit in an aperture, we are constraining the wave packet so that the photon, if detected downstream from the slit, is sure to have a wavelength within the range of wavelengths passed by the slit.

S. McGrew
  • 24,774
  • Re, "It's not just that the properties are not known; the properties don't have a value." Why is it more satisfying to say it that way instead of saying that, even though the theory makes accurate predictions about the statistical population of photons in the experiment, it says nothing about individual photons? – Solomon Slow Dec 03 '18 at 17:16
  • The point is that a photon (or any other quantum particle) does not have a quantum state until the state is measured. The alternate view ("hidden variables"), that a particle has a state but we don't know what it is until it's measured, turns out to be incorrect, as is revealed by the statistics of the results of measurements on single particles (e.g., "single-photon" double-slit interferometry). In the context of this question, the quantum state that's being measured is wavelength, so I'm saying that a photon does not have a definite wavelength until the wavelength is measured. – S. McGrew Dec 03 '18 at 20:37
  • You say, "a photon...until the state is measured." But what photon are you talking about? You can't even know that there was a photon until its state is measured. You can predict how many photons will be detected in an experiment, and you can predict the spatial distribution and the energy spectrum of the detection events, but a theory that predicts where and when the next one will strike simply does not exist. Maybe I'm confused about what "photon" means. I'm thinking of something that can be counted by a detector, but maybe you're thinking of it as the wave function that predicts... – Solomon Slow Dec 03 '18 at 21:10
  • 1
    Some folks argue that the very idea of "photon" is misleading, and that the term should be abandoned. I think they are right, but I don't know what term to use instead. This is getting a bit off-topic. Would you like to move it to a chat room? – S. McGrew Dec 03 '18 at 21:23
  • @S.McGrew There’s no reason to get rid of the term photon and there’s no justification to assume they don’t exist. – Bill Alsept Dec 05 '18 at 02:02
  • A problem with the term is that to most of the people who use it, "photon" refers to a particle that starts in one place and is detected in another place. That misunderstanding leads to a cascade of further misunderstandings. – S. McGrew Dec 05 '18 at 06:25
  • @S.McGrew What proof do you have that it is a misunderstanding. You can derive any phenomena like Fringe patterns etc. based on the idea of a photon being a particle going from here to there. On the other hand it takes quite a bit of imagination and uncertainty to produce an alternate solution. – Bill Alsept Dec 05 '18 at 16:16
  • Example: two lasers, phase-locked, their beams combined by a prism. Interference fringes appear even when the beams are attenuated down far enough that single photon counts can be distinguished, but the fringes disappear when one beam is blocked. Any further discussion of this will be off-topic and should be moved to a chat room. – S. McGrew Dec 05 '18 at 18:31
  • @S.McGrew Patterns are created when real coherent photons coming from multiple sources convolute on a detection screen. If you only have one beam (one source) then of course the fringes disappear. We can take it to chat if you want to. Thanks – Bill Alsept Dec 05 '18 at 19:02
  • Chat at [https://chat.stackexchange.com/rooms/86679/photonforge]. Single-photon diffraction has been demonstrated many times. All it takes is attenuating the beams enough to ensure that there is, with high likelihood, only one photon in the setup at a time. Per your assertion the interference fringe contrast should reduce towards zero as the photon flux goes down to the range of ~1 per nanosecond. But it doesn't. – S. McGrew Dec 09 '18 at 02:37
  • @S.McGrew I tried getting into the chat room but it would not let me. Not sure what I’m doing wrong – Bill Alsept Dec 10 '18 at 05:44
  • You should be able to get in now. – S. McGrew Dec 10 '18 at 13:07
  • @S.McGrew "If we let it pass through a slit in an aperture, we are constraining the wave packet so that the photon, is sure to have a wavelength within the range of wavelengths passed by the slit." Imaging I place a detector at a certain distance D from the slit. If we go to the limit case where the photon is as monochromatic as possible, then its wave function tends to spread homogeneously through space and the probability of detecting it is the same everywhere. Will this mean that I can detect the photon in a time t<D/c ? – E.phy Aug 06 '19 at 12:49
  • Not sure I understand what you mean. The wave function is not homogeneous through space in that case. It varies in amplitude with distance from the slit. – S. McGrew Aug 06 '19 at 13:09
  • Also, "monochromatic as possible" would mean that the frequency is very narrowly constrained, which means that the wavefunction is very long (in the direction of propagation). This means that the moment the photon exits the slit is highly indeterminate, which makes your t highly indeterminate. – S. McGrew Aug 06 '19 at 13:27