12

Let $C$ be a smooth curve in $\mathbb{R}^3$ that lies entirely on its convex hull, $\cal{H}(C)$.

Under what conditions on $C$ is $\cal{H}(C)$ the union of developable surface patches?

I believe the patches are all ruled, but perhaps not developable?

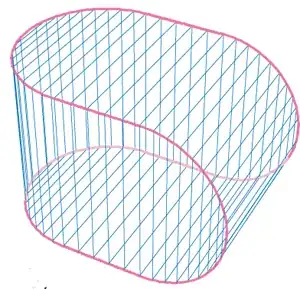
Example 1. $C_1$ is the concatenation of four semicircles as shown below. The surface patches are subsets of cylinders, or subsets of planes: developable.
           alt text

Example 2. $C_2$ is the curve studied by Ranestad and Sturmfels in "On the convex hull of a space curve," (arXiv link), and earlier studied by Sottile (who made the image below): $$x = \cos(\theta)\;,\; y = \sin(2\theta)\;,\;z = \cos(3\theta) \;.$$


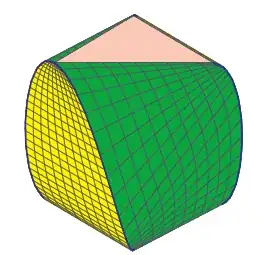
           Sturmfels & Stottle
Status (to me) unclear, despite its superficial similarity to the "tennisball" curve $C_1$ above.

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933

1 Answers1

14

For any point $P$ of the surface there is a point $S$ on the curve, so that the segment $PS$ is on the surface${}^1$. Hence, the surface of the convex hull is a union of ruled surfaces. Let's choose one of them.

Any ruled surface has non-positive Gaussian curvature at each of its points (see e.g. this link).

But for any convex surface, the Gaussian curvature cannot be negative.

It follows that the surface has zero Gaussian curvature. Therefore, it is developable, by definition.

Hence, the answer is "always".

  1. There is a plane $\alpha$ through $P$, so that $\mathcal H(\mathcal C)$ is completely on one side of the plane. Then the plane $\alpha$ touches $\mathcal C$, say at a point $S$, otherwise $P\notin \mathcal H(\mathcal C)$. If $S\in \alpha\cap \delta \mathcal H(\mathcal C)$, $PS\subset \delta \mathcal H(\mathcal C)$, where $\delta \mathcal H(\mathcal C)$ is the boundary of $\mathcal H(\mathcal C)$.
Cristi Stoica
  • 4,304
  • 1
    Wonderful, Cristi! The implication is that one can construct paper models of these hulls, which was my motivation in asking. :-) – Joseph O'Rourke Aug 05 '12 at 13:59
  • Thanks. I thought that it is about paper models of such hulls, given your previous work, for instance about unfolding polyhedra. – Cristi Stoica Aug 05 '12 at 15:21
  • does that hold independent of the curve's fractal dimension? I doubt that a fractal curve of fractal dimension 2 (e.g. Hilbert curve of a "cubed sphere") has a developable convex hull – Manfred Weis Jun 10 '15 at 05:39
  • Doesn't that also answer "When is the convex hull of two space curves the union of lines?" i.e. the answer to that question is also "always" (at least for curves with fractal dimension 1)? – Manfred Weis Jun 10 '15 at 05:47
  • Yes, I think your both remarks are correct, @Manfred Weis. – Cristi Stoica Jun 11 '15 at 06:39