In the course of doing mathematics, I make extensive use of computer-based calculations. There's one CAS that I use mostly, even though I occasionally come across out-and-out wrong answers.
After googling around a bit, I am unable to find a list of such bugs. Having such a list would help us remain skeptical and help our students become skeptical. So here's the question:
What are some mathematical bugs in computer algebra systems?
Please include a specific version of the software that has the bug. Please note that I'm not asking for bad design decisions, and I'm not asking for a discussion of the relative merits of different CAS's.
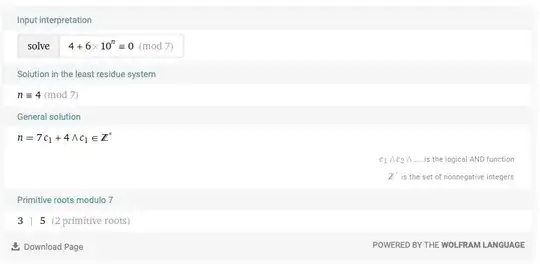
(designated as a bug by one of the Wolfram developers)
– Carlo Beenakker Sep 21 '14 at 14:04