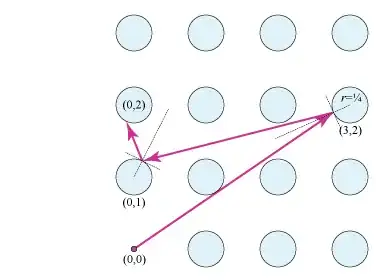
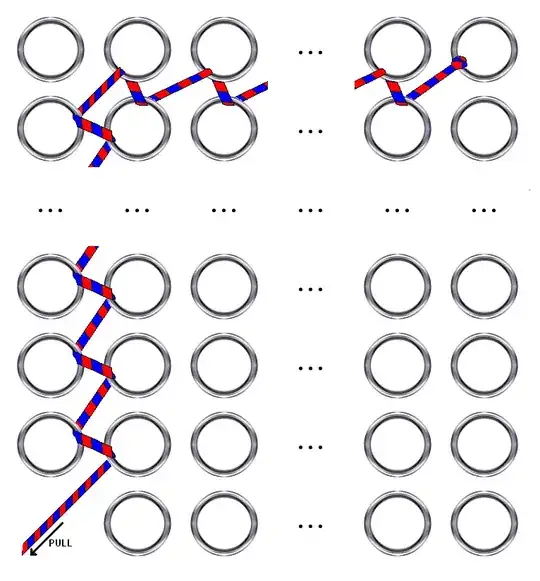
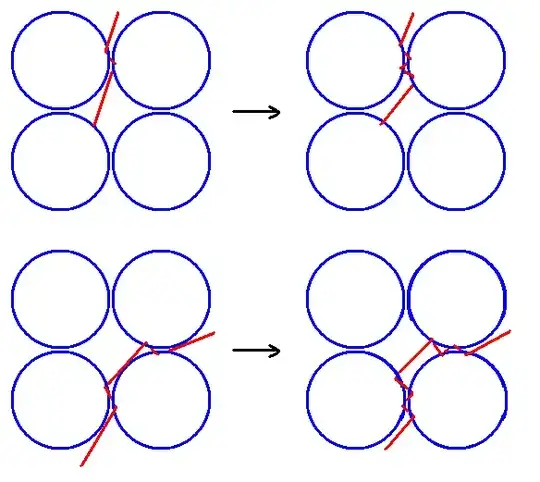
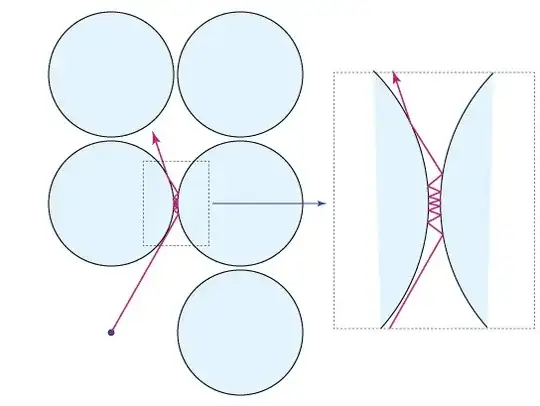
Let $C_r(x,y)$ or $C(x,y)$ be the circle of radius $r$ about the lattice point $(x,y)$.
Suppose we choose a sequence of circles to hit, and ask for the piecewise linear path of shortest length from the origin hitting each of the circles along the path. If this doesn't go inside a circle, then by the least action principle, the angle of incidence will equal the angle of reflection.
We can run into problems in two ways. First, the line segments can intersect other circles. For example, if we ask the path to visit $C(1,0)$ and then $C(3,0)$, then the line segment must intersect $C(2,0)$. So, we better restrict the paths not to do that. Second, the shortest piecewise linear path may pass through the interior of a circle. For example, from the origin to $C(1,1)$ to $C(2,2)$, the shortest path passes through the interior of $C(1,1)$. Again, to avoid this, we'll restrict the paths.
If $r$ is close to $1/2$, then you will need to bounce back and forth several times between adjacent circle to squeeze by them. However, for smaller $r$, we can construct a viable path more simply. Suppose $r \lt \sqrt{2}/4 \approx 0.354$. Then no line segment connecting $C_r(x,y)$ to $C_r(x+1,y+1)$ passes through any other circle. Consequently, from any point on $C_r(x,y)$ to any point on $C_r(x+1,y+1)$, the shortest path which hits $C_r(x+1,y)$ does not go inside $C_r(x+1,y)$, it is a piecewise linear path which reflects off of $C_r(x+1,y)$.
Take a path from $(0,0)$ to $(x,y)$ with unit steps parallel to the axes so that each step is perpendicular to the previous. Without loss of generality, we can assume $0 \le x \le y$, and we can walk to $(0,1), (1,1), (1,2), ... (x,x)$. From there, we use a sawtooth pattern: $(x,x+1), (x-1,x+1),(x-1,x+2),(x,x+2),(x,x+3),(x-1,x+3)... (x,y)$. Then the shortest curve starting at the origin which hits the circles centered at these points in this order is a piecewise linear path of a light ray which reaches $C(x,y)$ by reflecting off the circles in that order.

(Image added by J.O'Rourke)
This only handled $r \lt \sqrt{2}/4$. I believe that you can cover the case of $\sqrt{2}/4 \le r \lt 1/2$ by replacing $C(x,y) \to C(x+1,y)$ with $C(x,y)\bigg( \to C(x+1,y) \to C(x,y)\bigg)^n \to C(x+1,y)$, where the number of repetitions $n$ depends on $r$, perhaps $n=c/(1/2-r)$.