46

What is the behavior of Conway's game of life when the initial position is random? -- We can ask this question on an infinite grid or on an $n$ by $n$ table (planar or on a torus). Specifically suppose that to start with every cell is alive with probability $p$ and these probabilities are statistically independent. This question was motivated by a recent talk by Béla Bollobás on bootstrap percolation.

Many thanks for all the answers. A related question that I thought about is what is the situation for "noisy" versions of Conway's game of life? For example if in each round a live cell dies with probability $t$ and a dead cell gets life with probability $s$ and both $t$ and $s$ are small numbers and all these probabilities are independent.

Another example is to consider the following probabilistic variant of the rule of the game itself ($t$ is a small real number):

Any live cell with fewer than two live neighbours dies with probability $1−t$.

Any live cell with two or three live neighbours lives with probability $1−t$ on to the next generation.

Any live cell with more than three live neighbours dies with probability $1−t$.

Any dead cell with exactly three live neighbours becomes a live cell with probability $1−t$.

Following some comments below I asked about the computational power of such a noisy version over here.

Update: Related question Is there any superstable configuration in the game of life?

Community
  • 1
Gil Kalai
  • 24,218
  • 1
    Very interesting question. Presumably, something chaotic (like Brian's Brain), but with a much smaller density of gliders. – André Henriques May 31 '13 at 11:09
  • 4
    My experiments with GoL on a torus show that it eventually stabilises to a steady-state (modulo the alternating cross). You can see a video of one run at https://www.youtube.com/watch?v=tZTIiKcqdtI (the background is the same as what's happening on the torus). – Andrew Stacey May 31 '13 at 11:39
  • 1
    Could you perhaps be more specific about what you want to know about the behavior of the game of life with random initial configuration? – Algernon May 31 '13 at 12:10
  • 3
    Game of Life supports universal Turing machine that can even have self-replicating function. The Turing machine can run arbitrarily intelligent program. So, a question is "will the Game of Life universe with random initial position be filled with super-intelligent life forms, or will the chaos reign". I abstain from defining the meaning of "intelligent" :-) – Boris Bukh May 31 '13 at 13:13
  • 1
    @Algernon: does it with positive probability settle down to a 2-periodic state? Stronger: is there a fixed time N for which this is true? – Allen Knutson May 31 '13 at 13:27
  • 1
    @Allen: well, your question is surely interesting, but I don't see it anywhere in the OP's question. There is a wealth of interesting questions one can ask about the behavior of a cellular automaton on random initial configurations. Why e.g. not asking whether with positive probability every cell eventually dies out, which is more in the spirit of bootstrap percolation? – Algernon May 31 '13 at 14:21
  • 4
    @Andrew Stacey: It is rather naive to base an answer on experimentation. For example, there is a positive probability that somewhere in your system (lets take it to be infinite) you'll encounter this: http://en.wikipedia.org/wiki/File:Gospers_glider_gun.gif – André Henriques May 31 '13 at 15:39
  • 5
    @André Only on a mathematics forum could one argue that experimentation was no basis for assertion! Actually, I've yet to see a glider gun in my simulations so whatever that probability is then it'll be small. I suspect that it might be because it's on a torus so any glider gun that forms has a distinct possibility of shooting itself. – Andrew Stacey May 31 '13 at 19:23
  • 6

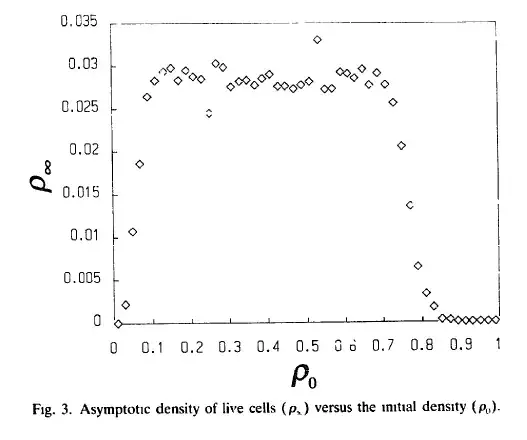
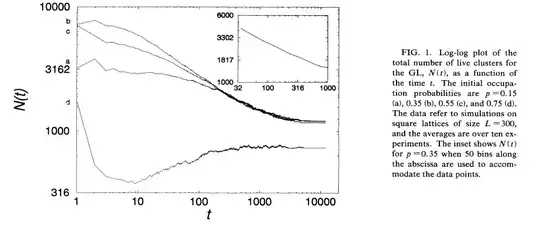
    so whatever that probability is then it'll be small< Let's say about $1−(1−(p^{20})(1−p)^{180})^{n^2/200}$. (I was too lazy to count the cells but you get the idea) Now here is the difference between a mathematician and a normal person. The mathematician believes that it is 1 and the normal person that it is 0. All existing computers are normal people, which makes it extremely hard to use them to do mathematics of this type...

     – fedja Jun 01 '13 at 00:23
  • 1
    Gil, regarding your "noisy" adaptation, it would also be natural to modify the game of life rules to be a probabilistic function of the neighboring cells, rather than a deterministic one. Thus, the likelihood that a cell turns on or off would be affected by it's current neighbors. For example, perhaps cells surrounded by 8 live cells have very little chance of still living, but those surrounded by only 4 have a greater chance (whereas in the deterministic version they definitely die), and cells with 1 live neighbor have a greater chance of spontaneous life than those with 0 live neighbors. – Joel David Hamkins Jun 05 '13 at 18:03
  • 1
    Ah, I see you mention this version in your question over at the other site. – Joel David Hamkins Jun 05 '13 at 18:26

7 Answers7

24

The most rigorous analysis of this that I know of is in:

N. M. Gotts. Self-organized construction in sparse random arrays of Conway's Game of Life. New Constructions in Cellular Automata, pp. 1–53. Oxford University Press, 2003.

In order to be able to actually prove something about what happens (in the face of undecidability results for general Life patterns) he considers the case of patterns that are very sparse (each cell initially alive i.i.d. with a very low probability $p$) for relatively short time scales (polynomial in $N=1/p$). Specifically, it looks from my reading that he calculates the asymptotic density of live cells for all times up to $N^{281/96}$, but cannot extend his methods past $N^3$ because somewhere between those two bounds events of unbounded complexity start dominating the density.

David Eppstein
  • 18,497
  • 4
    Fundamental undecidability is not necessarily an obstacle to proving theorems about what will happen probabilistically. For example, even with Turing machines (which surely exhibit a robust undecidability phenomenon), we know with asymptotic probability one as the number of program states increases that the behavior of a Turing machine program on a one-way infinite tape is completely trivial. See http://jdh.hamkins.org/haltingproblemdecidable/. For similar reasons, we might hope for advance also in the case of Life. Perhaps life is similarly decidable in most instances... – Joel David Hamkins May 31 '13 at 19:32
  • 8
    Remember that, with an infinite field, "most instance" include somewhere every possible finite pattern. In order to say something about denser configurations or longer numbers of steps we would need to resolve the question of whether it is possible for a pattern to exist that can survive and robustly reproduce itself in an environment filled with random junk. If they can exist, then they may eventually come to be a significant fraction of the population. On the other hand if they cannot exist, then it is plausible that more simplistic analysis techniques can be applied. – David Eppstein Jun 01 '13 at 01:00
  • @David Eppstein. I like very much your rephrasing of the question: this is exactly what one needs to think about. My bet is that the answer is "yes": there do exist patterns that can survive and robustly reproduce themselves (with an extremely low reproduction rate) in an environment filled with random junk. – André Henriques Jun 01 '13 at 13:54
  • 1
    One would also want to know whether there were finite patterns that progressively expand and obliterate everything in an environment filled with random junk. Perhaps such monsters grow (and merge?), leaving behind an expanding eye of calm emptiness inside the hurricane, which is pushed off to infinity. – Joel David Hamkins Jun 02 '13 at 00:38
  • 1
    @Joel: If such patterns exist, they will be roughly equi-distributed across space, and so your picture of "expanding eye which is pushed off to infinity" isn't quite correct. But indeed, what you are describing is a conceivable scenario. – André Henriques Jun 02 '13 at 16:22
  • André, what I had had in mind is that if you were standing at the origin (or wherever), you would eventually find yourself inside one of them, which expanded without bound around you. But actually I think that there is a big problem with this scenario, in the case of two of them merging, since if it is possible for them to merge, then it would also seem to be possible for them to be fooled into merging with a near copy that wasn't actually fully right, with the end result that the monster was killed or developed leaks that prevent it from functioning in the way I had described. – Joel David Hamkins Jun 02 '13 at 16:31
  • Agreed: I also don't think that the "monsters easting everything" scenario is a likely one. But it is one that one would need to exclude ... – André Henriques Jun 02 '13 at 17:44
  • Does anyone know an example of an 'interesting' configuration (e.g. one which replicates itself, or one which functionates as a universal Turing machine, or only a 'glider gun' etc.) and which is not vulnerable to arbitrary one-pixel damages? -- If such structures don't exist, I think it is rather unlikely that starting from a random configuration on an infinite grid much self-organization would take place. – Stefan Kohl Jun 02 '13 at 19:17
  • Stefan, it seems very likely that there would be a local stable configuration, which was not affected by whatever happened outside its borders. Imagine a kind of cell or even a wall (or a cell wall), which retained its own nature (on some periodic cycle), while being compatible with any possible boundary condition outside. In the random position, there would be such spores, which would survive no matter what else. I find it likely that there are such cells that also grow larger in some way. Perhaps they grow into each other, making the infinite life plane eventually a patchwork of cells. – Joel David Hamkins Jun 02 '13 at 20:37
23

The first study of the game of life with random initial conditions that I could find was this paper:

F. Bagnoli, R. Rechtman and S. Ruffo, Some Facts of Life, Physica A 171, 249 (1991) doi:10.1016/0378-4371(91)90277-J.

In it they attempt a kind of mean-field analysis (which I haven't digested) as well as do some numerical experiments which suggest that the system approaches a nontrivial asymptotic density for all $0\lt p\lt 1$.

Here's a plot from their paper of results on 256 by 256 toruses (their $\rho_0=p$):

figure 3 from Bagnoli, Rechtman and Ruffo 1991

They also investigated the temporal behavior, however I found more detailed simulations and discussion of scaling in this paper:

J. B. C. Garcia, M. A. F. Gomes, T. I. Jyh, T. I. Ren, and T. R. M. Sales. Nonlinear dynamics of the cellular-automaton ‘‘game of Life’’. Phys. Rev. E 48, 3345–3351 (1993)

Here is a plot showing the average number of connected clusters of live sites versus time.

figure 1 from Garcia et al 1993

They summarize their findings as follows (below $\varphi$ represents some quantity like the number of live clusters or the total number of live sites, etc.):

For initial occupation probabilities satisfying $0.15\leq p \lt 0.75$, each one of the different statistical functions $\varphi$ describing the dynamics of the GL may be divided in general in three intervals: First, a region extending from $t =0$ to $t\simeq L^{1/2}$ presenting large fluctuations in $\varphi$; second, a scaling region characterized by a power-law dependence between $\varphi$ and $t$, from $t\sim L^{1/2}$ to $t\sim L^{4/3}$ and finally the "steady state" or stabilization region (the SOC [self-organized criticality] state of Bak, Chen, and Creutz [4]) extending from $t\sim L^{4/3}$ to infinite and characterized by small fluctuations of $\varphi$ around some average value $\varphi_0$. These results are obtained from extensive numerical simulations on lattices with different values of L. The critical exponents obtained in the scaling region are robust and do not depend on $p$, for $0.15\leq p \lt0.75$. [...] For low initial occupation ($p\lt 0.15$) or high density occupation ($p \geq 0.75$) the scaling region disappears, and now the domain for large fluctuations of $\varphi$ extends from $t =0$ to $t\sim L^{4/3}$. This region is followed by the "steady state" characterized by small fluctuations around an average value.

I didn't see any rigorous arguments in the papers I found but that doesn't mean there aren't any out there. In particular as Gil hints there is a strong connection to bootstrap percolation, and perhaps some of the theorems proven there apply here as well.

j.c.
  • 13,490
15

The asymptotic dynamics of the Game of Life from a random starting field is unknown, and profoundly so. Experiments on small fields for small numbers of generations suggest that the asymptotic density is on the order of 1/20 for a wide range of initial probabilities. But these small experiments cannot answer the big questions. Perhaps there exists a high-density starting pattern that fits in a 1000x1000 square, which aggressively takes over the plane with copies of itself. If such a pattern exists, then it will occur with certainty in any random field that is large enough (say 2^(10^8) on a side). If it occurs, it takes over, and the asymptotic density will be much higher than 1/20.

Researchers disagree on whether such a "cancer" is possible (it would have to defend itself against "background radiation" emitted by its environment). The last time I talked to Gosper on this subject, he was convinced that it is possible; if he is right (and one bets against Gosper on such matters with great caution) then the long-term dynamics of the Game of Life is complicated and Darwinian.

ACW
  • 151
  • 3
    If you think there is a high-density cancer, then wouldn't you also find it reasonable to think that there could also be a less-dense cancer? In that case, one would expect both such kinds of cancers would appear in the random position, and so the eventual position would be one without a convergent asymptotic density, having pockets of various densities intertwined amongst one another unboundedly. – Joel David Hamkins Jun 06 '13 at 02:07
4

I see no reason to expect a different answer to the questions:

(1) "What is the behavior of John Conway's Game of Life when the initial position is random?"

and

(2) "What is the behavior of Brian Silverman's Brian's Brain when the initial position is random?"

I therefore propose (2) as an alternate to Gil Kalai's question. The complexity of the Brian's Brain's is more visible at human time/space scales and, presumably, computer simulations can be trusted more than for Game of Life.
    It would be great if anyone could prove that a random initial position of Brian's Brain on an infinite grid results with almost certainty in a pattern that remains always non-empty as time goes to infinity? I suspect however, that this is a difficult problem.

André Henriques
  • 42,480
  • At least as observed for moderate size starting fields and relatively high densities of initial cells, Life tends to stabilize to scattered still lifes and oscillators, with longer-lived chaotic regions whose frequency is monotonically decreasing with time. If there are no replicators that can survive in junk etc., then in Life it seems plausible that with probability 1 any given cell eventually becomes periodic, although this is currently out of reach of proof. In contrast, Brian's Brain seems to stay chaotic for all time. So qualitatively they are very different. – David Eppstein Jun 13 '13 at 23:52
  • What about glider guns? Strictly speaking, they don't replicate themselves, but they create junk... which might result (with a lot of luck) in the occurrence of another glider gun somewhere else far away. For "moderate size starting fields", I am of course forced to agree with you... but that's not what I had in mind when I wrote this answer. – André Henriques Jun 14 '13 at 11:15
  • I think that, in fields of the typical sort of junk left over from a high-density random start, that a sequence of gliders fired into the junk (from a gun surrounded by empty space) will fairly quickly cause gliders to come back along a reverse track (endangering the gun). Over longer time scales the glider stream will cause the junk to slowly grow into the empty space, endangering the gun in a different way. So more active countermeasures would be needed to allow such a pattern to live and reproduce itself. – David Eppstein Jun 14 '13 at 18:25
4

About the random version, a relevant reference is (IIRC):

Peter Gacs, Reliable computation with cellular automata. Journal of Computer System Science, 32(1):15–78, February 1986. Conference version at STOC’ 83.

(As well as subsequent works.) Essentially given a Turing-complete automaton - not sure about the terminology here - it can be made robust to noise by adding error-correction mechanisms. It is not about GoL, and tastes a bit more like low-temperature Glauber dynamics mixed with directed percolation, but the ideas might be relevant here.

Vincent Beffara
  • 1,761
3

In the probabilistic scenario it seems unlikely that the density will be arbitrary low. As soon as the system would approach this state the would be a lot of empty space with infinitely many small living configurations. Several of these will be in space filling configurations. The small t value should then not be able to prevent a significant growth due to these configurations.

Heijne
  • 71
0

It seems there is an easy solution to the „probabilistic variant of the rule of the game itself”.

If we ask about the situation after the infinite number of steps, the answer is: the system will end up in its absorbing state “all cells dead”.

First observe that in the „probabilistic variant of the rule of the game itself”, the state “all cells dead” is really an absorbing state - no cell has a chance to become live again.

Now, observe that in any current state, there’s always a non-zero probability of the next state being “all cells dead”. Each living cell in step t can be dead in step t+1 and each dead cell in step t can be dead in step t+1 with non-zero probability.

With infinite number of steps, an event with non-zero probability in every step will happen with probability one in some step.

The above is a general idea. To be more precise we should talk about asymptotic density of living cells being zero and not about ending up in a state of “all” cells being dead. Probably, the best way to start the analysis of the infinite grid case is to observe that in any step there’s a non-zero probability of the next state having arbitrarily low density of living cells. For further discussion see the comments below.

helper
  • 166
  • 1
    If the number of cells is finite, yes. -- But if we have an infinite grid as assumed in the question, your argumentation works only for any finite part of the grid -- or am I missing something? – Stefan Kohl Jun 09 '13 at 12:42
  • 1
    I think of the infinite grid as infinitely many finite grids (“regions”). If each region tends to its absorbing state, the system (infinite grid) tends to a state where the density of living cells is approaching 0. Moreover, when the density of living cells is very low, the interaction between regions vanishes. You need 3 cells on the border of a neighbor region to “give birth” in a given region. There'll be infinitely many regions with some living cells. I see this fact as similar to e.g. the fact that there are infinitely many primes but their density is zero. Is my argument correct? – helper Jun 09 '13 at 22:02
  • 1
    @helper: I don't agree with you. You say: "I think of the infinite grid as infinitely many finite grids (regions). If each region tends to its absorbing state, the system (infinite grid) tends to a state where the density of living cells is approaching 0". You assume that the speed at which a finite region tends to the empty state is greater than the speed at which information flows between the various finite regions. But I don't think that that's a correct assumption. – André Henriques Jun 09 '13 at 22:11
  • 1
    @André Henriques I also say "when the density of living cells is very low, the interaction between regions vanishes. You need as many as three cells on the border of a neighbor region to “give birth” to a previously dead cell in a given region." – helper Jun 09 '13 at 22:19
  • 1
    @André BTW, can’t we simply state that sooner or later, the system has to reach a state of arbitrarily low density? From now on, we don’t have to worry very much about the speed at which information flows between the various finite regions. – helper Jun 09 '13 at 22:39
  • 2
    @helper The argument is definitely wrong. There are processes (e.g. the contact process with high enough propagation rate, or "slices" of directed percolation) which die in any finite volume for the reason you mention, but nevertheless admit invariant distributions with positive asymptotic density. – Vincent Beffara Jun 11 '13 at 17:11
  • 1
    @helper To give a more "physical" intuition: the time needed for a box to die out will typically be exponential in the volume of the box (that's what it takes for each cell to die at the same time), while the time for a neighbouring box to make you alive again is linear in the diameter (propagation fronts move linearly). So even if one of the regions were to die out (which it will), there may be plenty of "life reservoirs" in the vicinity to resuscitate it before they themselves die. – Vincent Beffara Jun 11 '13 at 17:15
  • 1
    @Vincent Thank you very much that you invested your time to explain this to me. If you could point me to the reference for the processes you mentioned I’d be grateful. Nevertheless, I think we could agree that there’s still a possibility that the asymptotic density of the analyzed variant is 0 - you wrote “there may be” not “there have to be”. Personally, I believe in the conjecture of zero asymptotic density but cannot prove it. I don’t believe in “life reservoirs” being typical. […] – helper Jun 11 '13 at 19:44
  • @Vincent […] There’s no reason to expect plenty of infinitely growing patterns (like guns or puffer trains) created by random initial configuration. Perhaps one day in the future my “definitely wrong argument” can be made a part of a larger proof that noisy rules of GoL lead to the zero density of living cells. Maybe you know this kind of proof in percolation theory or somewhere else? Once again, thank you Vincent. I look forward to read sth about the processes you mentioned. – helper Jun 11 '13 at 19:44
  • 1
    @helper Sure, I did say "there may be", and it is quite possible that indeed density would always go to zero. I was simply pointing out that what you said could not be enough, because it did not use the specifics of GoL. And in general it is quite hard to tell what happens for a given model ... – Vincent Beffara Jun 11 '13 at 23:04