8

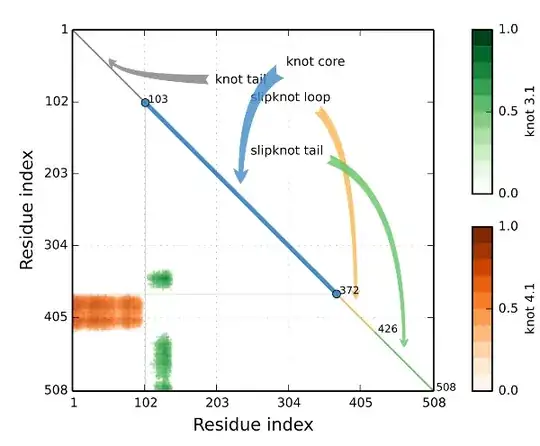
Let $\gamma$ be a simple (non-self-intersecting) open curve in $\mathbb{R}^3$. I am seeking a measure of its degree of "entangledness," some measure that accords with the intuition one senses with a tangled fishing line. One measure is to connect the two ends of $\gamma$ and use a measure of its degree of knottedness, e.g., its unknotting number, or, perhaps, its writhing number. But it would seem these depend on how the ends are connected, rather than on $\gamma$ alone. Have other natural measures been proposed? I'd appreciate pointers. Thanks!

       Tangle
A year later, I remain interested, especially in some type of energy measure along the lines attempted by Qfwfq. It would be especially pleasing to have a measure that somehow measures the effort it would take to straighten a tangle.
j.c.
  • 13,490
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 1
    Consider all rotations of the curve in $\mathbb R^3$ and all linear planar projections. Take the minimum of the number of crossings over all such projections. What do you think of that? – Ryan Budney Jun 01 '13 at 15:13

3 Answers3

6

Ken Millett has worked on measures of knottedness for open curves. See e.g. this book chapter. The basic idea that he and collaborators have been exploring is to try to define a kind of "dominant knot type" from trying out a large number of ways of closing up the chain.

update: KnotProt is an online database of "knotted proteins", which catalogues the roughly 1100 protein structures from the PDB which exhibit knottedness according to the above idea:

[...] we connect protein endpoints several hundred times to two points randomly chosen from a set of vertices of the truncated icosahedron (i.e. a polyhedron representing, e.g. the geometry of C60 fullerene) positioned on a large sphere enclosing the analyzed chain. Subsequently these two points are connected by an arc lying on the surface of the sphere. The most frequently observed knot type for a given analyzed chain is then associated with that chain as its dominant knot type.

What's more, given a protein chain of length $N$, they also analyze all $N^2$ possible connected subchains parametrized by varying the start and end, thus giving a "fingerprint" for knotted subregions of proteins.

Here's one example, protein 2WSW.

fingerprint protein

The 2015 paper (by Jamroz, Niemyska, Rawdon, Stasiak, Millett, Sułkowski and Sulkowska) discusses further details and gives more references to other work.

j.c.
  • 13,490
  • Thanks, jc, it does make sense to use statistical properties of all possible closures. In their case, they connect each endpoint by a segment to a point on a large surrounding sphere. – Joseph O'Rourke Jun 01 '13 at 18:18
6

Peter Roegen works on this problem, with the practical goal of effectively identifying certain knotted proteins. His descriptors (not "invariants", because open curves are topologically unknotted) are Gaussian integrals, and give real-number analogues of finite-type invariants for open curves. The simplest of these is the self-linking number, which is the average (integral) over all rotations of overcrossings minus undercrossings.

To my mind, Gaussian integrals do indeed seem the most natural descriptors for open curves, because they don't artificially close them. They are also quite powerful- they are the practical descriptors of choice for certain classes of knotted proteins. The results and effectiveness of the simplest of these descriptors are summarized in this poster.

Daniel Moskovich
  • 21,887
3

Perhaps, one could define the "entangledness" of an open curve (of unit lenghth and parametrized in arclength) as the minimum

$$\mathrm{min}_{H}\;E(H), $$

over all possible smooth simple "strightening" homotopies $H:[0,1]\times [0,1]\to\mathbb{R}^3$ with $H(0,s)=\gamma(s)$ and $H(1,s)=s\cdot \gamma\;'(0)+\gamma(0)$ $\forall s\in[0,1]$, of the total work (energy) $E(H)$ needed to strighten up the curve, supposing the curve has an evenly distributed unit mass:

$$E(H)=\frac{1}{2}\int_0^1\int_0^1|\frac{\partial H}{\partial t}(t,s)|^2\;dt\;ds$$

I'm not aware if this idea has been made effective somewhere in the literature...

Qfwfq
  • 22,715
  • 1
    This is an intriguing idea, Qfwfq! – Joseph O'Rourke Jun 01 '13 at 18:21
  • Perhaps, in order to factor out irrelevant movements of the "string", instead of $H(1,s)=(s,0,0)$ one could define $H(1,s):=s\cdot \gamma'(0)+\gamma(0)$, $s\in [0,1]$, otherwise the minimum is not invariant under rigid motions of $\mathbb{R}^3$. I'll edit accordingly. – Qfwfq Jun 01 '13 at 19:58
  • Yet it's not clear whether strightening w.r.t. the first end needs the same amount of energy as strightening w.r.t. the second end (i.e. minimizing under the condition $H(1,s)=s\cdot \gamma; ' (1)+\gamma(1)$)... – Qfwfq Jun 01 '13 at 20:03
  • (...But one could always take the minimum between the two quantities to make the result end-invariant) – Qfwfq Jun 01 '13 at 20:05
  • Interesting: This reminds me of various $L_p$ metrics on groups of symplectomorphisms, see e.g. http://www.math.vanderbilt.edu/~brandem/LpMetricTwoSphere7.pdf and references therein. The difficulty is to get interesting lower bounds for such energy functional. In the symplectic ($L_2$-metric on $Ham(S^2)$) context, people use braid groups for this purpose. – Misha Jun 01 '13 at 20:29
  • Qfwfq: Alas, it seems that your definition does not work, as the quantity $min_H E(H)$ is bounded above by a constant independent of the curve. See Theorem 2.1 in A.Shnirelman, "Generalized fluid flows, their approximation and applications", Geom. Funct. Anal. 4 (1994), no. 5, 586-620. – Misha Jun 05 '13 at 00:15
  • Then is it possible that a sensible measure of entangledness is how near $\mathrm{min}_H E(H)$ reaches that constant from below? Or maybe I missed the point? - Otherwise I stand corrected. :) – Qfwfq Jun 05 '13 at 08:34
  • 1
    Qfwfq: I am not sure that would work either, but another thing to try would be p-energy for other p's. The trouble is, it is conceivable that $inf_H E(H)$ is zero for every open string! One can probably learn quite a bit from Shnirelman's paper (I did not read it closely), maybe his proof works for other p's too and maybe it can be used to establish vanishing, since what Shnirelman is proving is quite a bit stronger: Given a self-diffeomorphism f of a cube, he bounds from above minimal energy of isotopy from f to the the identity. – Misha Jun 06 '13 at 00:01