10

Kanamori in the introduction of his book "The Higher Infinite" says:

"The investigation of large cardinal hypotheses is indeed a mainstream of modern set theory, and they have been found to play a crucial role in the study of definable sets of reals, in particular their Lebesgue measurability. Although formulated at various stages in the development of set theory and with different incentives, the hypotheses were found to form a linear hierarchy reaching up to an inconsistent extension of motivating concepts."

My question simply is:

Question: Is the tree of large cardinals linear? Precisely: Are there four large cardinal axioms like $\text{A}, \text{B}, \text{C}, \text{D}$ such that at least one of the following diagrams be true?

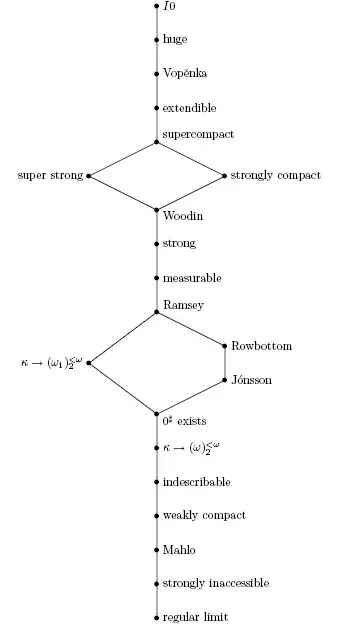
enter image description here

Note that in the current tree of large cardinals one can find some diamonds like above diagrams but we usually interpret this phenomenon as "unknown" situation not a possible "incomparablility" between large cardinal axioms. For example note to the following diagram:

enter image description here

  • 6
    For the benefit of color blinded people, try to avoid mixing green and red in the same diagram (especially if these are the only colors you are going to use). Dotted arrows and full arrows are better. – Asaf Karagila Nov 15 '13 at 21:56
  • In light of the fact that "($p$ implies $q$) or ($q$ implies $p$)" is a propositional tautology, perhaps you should clarify what you mean by the red arrows. I think what you mean is that (under some assumption), the implication $p\to q$ is not provable or something like that. – Joel David Hamkins Nov 15 '13 at 22:29
  • 1
    @JoelDavidHamkins: By "$\text{ZFC+B}$ doesn't imply $\text{ZFC+C}$" I mean the theory of $\text{ZFC+B+$\neg$ C}$ is consistent. By $Con(\text{ZFC+B})$ doesn't imply $Con(\text{ZFC+C})$ I mean it is consistent with $\text{ZFC}$ that "there exists a model of $\text{ZFC+B}$ but there is no model for $\text{ZFC+C}$". –  Nov 15 '13 at 22:52
  • @AsafKaragila: Dear Asaf, your comment carries the sprite of my soft question on math.stackexchange.com, I am really happy to see that you pay enough attention to those who have some disabilities. I will change the diagram as soon as possible. Thank you for your notification. –  Nov 15 '13 at 22:59
  • @AsafKaragila: I fixed the problem in diagram. Thanks again. –  Nov 15 '13 at 23:11
  • 2
    I pay attention to my disabilities. – Asaf Karagila Nov 16 '13 at 06:06
  • @AsafKaragila: I am so sorry to know about it. But I think you are one of the mathematicians who I called hero in my soft question. –  Nov 16 '13 at 12:03
  • @AsafKaragila: I don't know why but I think perhaps my question in writers forum could be interesting for you. I will be happy to know your idea about it. –  Nov 16 '13 at 12:14
  • I wish people catered to the needs of intellectually limited ones like myself... but that's life.. – plm Sep 01 '23 at 05:46

2 Answers2

10

Let me just add to Andres excellent answer that The $\Omega$-conjecture of Hugh Woodin implies that all large cardinals are wellordered under the relation "implies the consistency of". This is a major line of investigation in Inner Model Theory. I recommend Woodin's "Suitable extender Models" (the introduction provides motivation to this problem).

Rachid Atmai
  • 3,756
8

This is the key question pursued by inner model theory. As far as we can prove, the consistency strength order is indeed linear (indeed, a pre-well-ordering), and we expect this will continue to be the case, at least as far as the large cardinals we currently use goes.

Rather than repeating myself and others here, let me make a suggestion: You can learn more about the consistency strength hierarchy in the writings and talks of John Steel, many of which are available at his webpage. There are also many answers on this website (by myself and others) addressing this question (for example, see here).

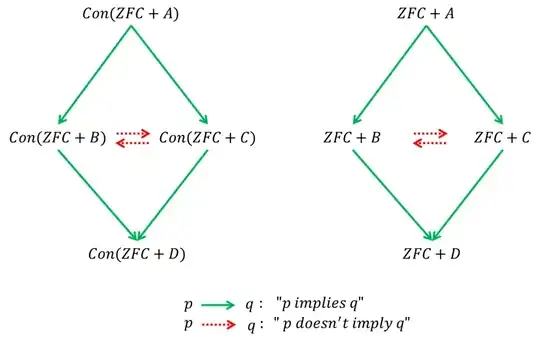
You should keep in mind that the right comparison is in terms of consistency strength, not in terms of outright implication or size. For example, the existence of $0^\sharp$ is a large cardinal statement, but it does not even imply the existence of inaccessible cardinals. However, it implies a proper class of weakly compact cardinals (and more) in $L$. Similarly, the first Woodin cardinal is not even weakly compact, but it implies the existence of many smaller weakly compacts. And the least strongly compact cardinal can be the first measurable, and it may exist in a universe without strong cardinals, though in consistency strength it is significantly beyond measurability or strongness.

All that being said, one can always come up with artificial large cardinal statements, coding Gödel-like statements that make them incomparable. It is understood that this is not what we are discussing here. Of course, there is a somewhat inherent vagueness in this claim, since I am not formally defining large cardinal, much less "natural" large cardinal. Consider it an empirical fact. But it is not just data without evidence. We have a significant body of results indicating that this ought to be the case.

Nor should you think this is exclusive to "large cardinals": The consistency strength hierarchy is much richer. We go from one rung of the ladder to the next by replacing a (sound) theory $T$ with $T+\mathrm{Con}(T)$, for example. This only takes us so far, and we have a significant jump if we require the existence of an $\omega$-model of $T$. And yet another significant jump if we ask for a transitive model.

Community
  • 1
Andrés E. Caicedo
  • 32,193
  • 5
  • 130
  • 233
  • 1
    Andres, you say that "As far as we can prove, the consistency strength hierarchy is indeed linear", but in light of the situation with strongly compact cardinals and other large cardinals whose relation is not yet clearly linear, what do you mean? For example, would it also be correct to say, "as far as we can prove, the consistency strength hierarchy is not linear"? – Joel David Hamkins Nov 15 '13 at 22:27
  • 1
    Hi Joel, I mean: Given any statement that we have studied, we can either locate it precisely on the hierarchy, or we expect that once inner model theory and forcing develop enough, we will. This means that we have reasonable upper and lower bounds on the strength of the statement, given our current tools, sometimes very precise in the presence of additional assumptions we expect to eventually suppress. – Andrés E. Caicedo Nov 15 '13 at 22:53
  • What we do not have is even a scenario the outcome of which would be incomparable statements. For strongly compact cardinals, for example, we know that in lower bound they are as high as inner model theory can currently prove. We do not anticipate any surprises there. Our current tools are reasonably robust once our statements are strong enough, meaning, we are no longer dealing purely with comparisons at the $Pi^0_1$ level, but have many descriptive set theoretic tools at our disposal and, likewise, bounds establish significantly stronger results than mere consistency strength comparisons. – Andrés E. Caicedo Nov 15 '13 at 22:59
  • 6
    Well, I agree that all our tools are set up to prove instances of linearity. But wouldn't it be a confirmation bias error to deduce from this that the entire hiearchy is linear? We simply lack tools for proving non-linearity, and so naturally we don't often see that. It is conceivable to me even that the obstacles to progression in the inner model theory may result in part from non-linearity. The "scenario" for non-linearity here may be exactly what we've been observing, namely, long-standing open questions about the comparative strength of certain large cardinal notions. – Joel David Hamkins Nov 16 '13 at 00:19
  • @Joel: Your argument is reasonable. The fact that we cannot see a non-linearity doesn't imply that we cannot find such phenomenon in future. We need a rigorous proof for the linearity of the tree of the large cardinals. I think the situation in this case is really complicated and needs more researches. –  Nov 16 '13 at 02:05
  • I want to point out that there are two reasonable large cardinals proposed very near the top. Both extend $I_1$ and involve incorporating more AC to the target model, specifically a non-trivial instance of uniformization holds in those models. Both are proposed by Laver and at least one is sensitive to small forcing, so it violates the Levy-Solovay theorem in an "unusual way". I stated the forcing-fragile axiom in a question here on MO. The other can be found in Woodin's Suitable Extender Models II, def. 1. It's not clear how these axioms relate to $I_0$ or Woodin's $E_\alpha$-sequence. – Everett Piper Nov 16 '13 at 02:37
  • 1
    Andres, or anyone, could you give a reference or point me to a write-up of how "one can always come up with artificial large cardinal statements, coding Gödel-like statements that make them incomparable"? Thank you. – user40919 Jan 07 '14 at 16:48