What stories, puzzles, games, paradoxes, toys, etc from everyday life are better understood after learning homology theory?
To be more precise, I am teaching a short course on homology, from chapter two of Hatcher's book. Before diving into the details of Delta-complexes, good pairs, long exact sequences, degrees, and so on, I would like to present a collection of real-life phenomena that are greatly illuminated by actually knowing homology theory. Ideally, I would refer back to these examples as the course progressed and explain them with the new tools the students learn.
Here is what I have thought of so far.
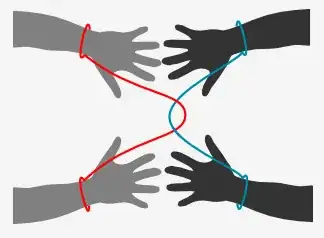
- Tavern puzzles: before trying to solve a tavern puzzle, it is always a good idea to check that the two pieces are topologically unlinked. You can approximate this by computing the linking number, via the degree of the map from the torus to the two-sphere.
- Cowlicks: after getting a very short haircut, there is a place on your scalp (typically near the crown) where the hair is standing up. This is "explained" by the hairy ball theorem: a tangent vector field on the two-sphere must vanish somewhere. "Explained" is in quotes because your hair is a vector field on a disk, not on a sphere.
- When you knead dough, and then push it back into its original shape, there is always a bit of dough that has returned to its original position. This is the Brouwer fixed-point theorem. This example is a bit tricky, because it is impossible to see the fixed bit of dough. (Now, when you are hiking, you can clearly see that there is a point of the map lying directly above the point it represents. However, this is better explained by the contraction mapping principle.)
- There are no draws in the board game Hex. This is equivalent to the Brouwer fixed-point theorem. This isn't a perfect example, because most people don't know the game.
Noticeably missing are puzzles, etc that rely on homological algebra (diagram chasing, long exact sequences, etc).
$\newcommand{\SO}{\operatorname{SO}} \newcommand{\ZZ}{\mathbb{Z}}$ EDIT: Let me also give some non-examples, to clarify what I am asking.
- Linking number also arises in discussions of DNA replication; see discussions of topoisomerase. However DNA is not an everyday object, so doesn't work as an example.
- The plate (or belt) trick; this is a fancy move that a waiter can make with your plate, but it is more likely to appear in a juggling show. It is explained by knowing $\pi_1(\SO(3)) = \ZZ/2\ZZ$. However, this is a fact about the fundamental group, not about homology.
- Impossible objects such as the Penrose tribar that exist locally, but not globally. These can be explained via non-trivial cohomology classes. But, cohomology is in the next class, so if/when I teach that...