6

Let $K$ be a solid, homogenous convex body in $\mathbb{R}^3$. Place $K$ on an inclined plane, and let it roll down the plane, under some reasonable assumptions of friction between $K$ and the plane, and tilt angle of the plane, so that it rolls without slippage under the influence of gravity. Let the $y$-axis represent straight down the gradient of the plane, and $x$ the distance of the contact point(s) to the left or right of straight-down.

Q. Does there exist some $K$ so that, from a particular starting position, $K$ rolls such that the sideways displacement $x$ grows without bound the further down $y$ it rolls?

For example, perhaps there is a $K$ so that this (entirely fanciful) sideways "crab-walking" path is the trace of the point of contact:
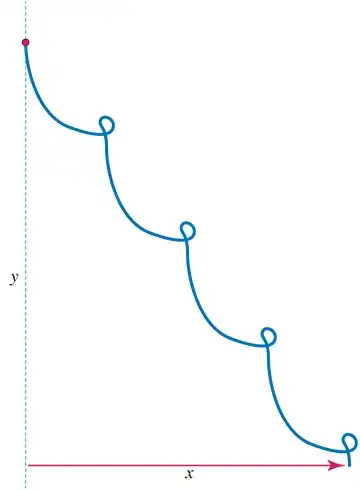
          RollingPathCrooked
Or perhaps no such $K$ exists—It is mathematically impossible? I neither have strong intuitions here, nor a clear idea on how to settle the question one way or the other. I have no particular candidate $K$, although this asymmetric oloid-like object is what piqued my interest:


          Oloid12_36

Community
  • 1
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 4
    Doesn't a circular cylinder do this, if you start it at an angle with respect to straight downhill? Perhaps I've misunderstood the question. – Joel David Hamkins Apr 17 '14 at 03:47
  • @JoelDavidHamkins: I don't see how to alter the question to exclude the cylinder, but that is not what I meant. :-) What I sought you found at MoMath. Thanks! – Joseph O'Rourke Apr 17 '14 at 10:28
  • Could you tell me what is the precise meaning of "homogeneous body" in your first sentence? – Joel David Hamkins Apr 17 '14 at 13:21
  • @JoelDavidHamkins: I meant composed of a uniform material, i.e., not like loaded dice, with one interior portion including more dense material than another interior portion. – Joseph O'Rourke Apr 17 '14 at 13:43
  • 1
    Ah, that makes sense. Thanks! Incidentally, the MoMath exhibit also includes some extremely interesting non-convex shapes that roll in a very interesting way. The goal for participants is to get the shape to follow the pattern inscribed on the inclined table as it rolls, and it is challenging to get it exactly right. I think I've spent hours there in total. – Joel David Hamkins Apr 17 '14 at 13:47
  • 1
    @JoelDavidHamkins: Perhaps I should modify the question to require the initial vector of motion to be straight down $y$---roughly as in the drawn contact path. This would exclude the cylinder and many other examples. – Joseph O'Rourke Apr 17 '14 at 15:52

1 Answers1

16

The answer is yes, and you can play with them at MoMath. Specifically, the Twist and Roll exhibit has several convex shapes, which will roll arbitrarily far sideways when started at an angle that is not directly downhill.

Click the image to see a video of the exhibit, which shows the motion of several of the objects.

Community
  • 1
Joel David Hamkins
  • 224,022