49

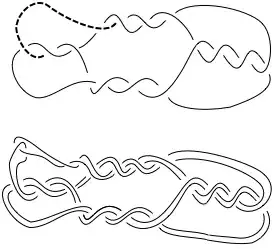
It is well known that knot diagrams cannot be monotonically simplified using Reidemeister moves. For instance, the Goeritz unknot cannot be directly simplified. On the other hand, there is a stronger move that 3-manifold topologists sometimes use, called the "under move": take a section of the knot that has only under crossings, and replace it with another under-strand connecting the same two endpoints. We can use this to simplify the Goeritz unknot one step:

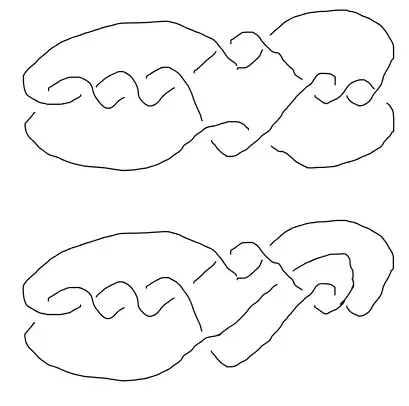
Simplifying the Goeritz unknot using an under move

Question: Can every diagram of the unknot be monotonically simplified using only under moves (or maybe under and over moves)?

Probably one needs to allow level moves as well.

This is related to an earlier question: Are there any very hard unknots? My move is more precise than that one, and Haken's "Gordian knot" can be simplified at least one step using a few level under-moves and then a reducing under-move on the right-hand side.

(I was wondering about this during a talk by Prasolov on his amazing work with Dynnikov on similar questions in the context of grid diagrams. Surely someone has considered this before.)

Community
  • 1
Dylan Thurston
  • 10,033
  • 1
    I'd imagine you could ensure over/under moves are insufficient by doing something like a Whitehead doubling operation on your original knot. Or a cabling. – Ryan Budney Oct 08 '14 at 22:36
  • 2
    A more general question: Is there some (natural) set of moves that can monotonically simplify any knot? – Joseph O'Rourke Oct 08 '14 at 23:00
  • 1
    Just to clarify, by "monotonically simplified" is your complexity function for knot diagrams crossing number? – Neil Hoffman Oct 09 '14 at 01:20
  • Ryan, I don't see how Whitehead doubling would make the under move obviously insufficient. If I have two parallel strands and I want to move them around, I can do under moves on them one at a time, no? – Dylan Thurston Oct 09 '14 at 03:53
  • 4
    Joe, that more general question is basically Gowers' question in the earlier question I linked to. Basically the answer is no one has one for knot diagrams, but grid diagrams provide an alternate setting where the answer is yes. (But you also contributed to that discussion, so I guess you know this.) – Dylan Thurston Oct 09 '14 at 03:55
  • Neil, yes, that's what I intended. – Dylan Thurston Oct 09 '14 at 03:55
  • 1
    What about this other one of Haken? https://dl.dropboxusercontent.com/u/8592391/public_html/hakenunknot1.jpg – Ian Agol Oct 09 '14 at 05:17
  • 2
    @IanAgol: If I don't misinterpret the diagram, there is an over move that reduces the number of crossings by 2: look at the rightmost upper corner and take that whole horizontal strand and slide it down to the bottom. If you're careful, you go from crossing four double-strands to crossing three. – Marco Golla Oct 09 '14 at 07:22
  • @IanAgol, Marco, I also see an under move that does a similar thing, with a horizontal strand near the upper-left. Ian, where do you get these great pictures? – Dylan Thurston Oct 09 '14 at 13:09
  • 4
    Gordon gave them to me a long time ago when I was a grad student thinking about grid diagrams of unknots. I think Doyle told me that Conway had a belief that one could untie an unknot using the sorts of moves you describe. I'm not sure this question ever got in the literature, but I suspect it is still open. If the strict decreasing moves worked, it would probably give a polynomial unknotting algorithm. But it's not so clear if there is only monotonic simplification. – Ian Agol Oct 09 '14 at 14:02
  • @IanAgol, it's easy to look for strict decreasing moves (consider each understrand, and do a shortest-path algorithm to see if it improves things). But I don't think that does work. It would still be interesting, however; for instance, it would give bounds on the total number of crossings you need to introduce using Reidemeister moves. – Dylan Thurston Oct 09 '14 at 14:18
  • Ochiai's unknot is an example in which strict decreasing moves do not improve things (unless you allow also level moves): http://en.wikipedia.org/wiki/Unknotting_problem#mediaviewer/File:Ochiai_unknot.svg – Daniel Moskovich Oct 27 '14 at 10:10
  • Yes, there have been several examples above where you need level moves, including the Goeritz knot in the original post. Ochiai's example looks nice and simple. – Dylan Thurston Oct 29 '14 at 13:22
  • Just for fun, the unknot here has a tangle diagram with a cycle of bigons, which suggests a sequence of flypes that unknot it rather quickly. – Jesse C. McKeown Nov 03 '14 at 19:18
  • Just now realizing that these under moves generalize all three Reidemiester moves. So the under move generates knot equivalence all by itself. – Akiva Weinberger Oct 26 '21 at 14:34

2 Answers2

18

This is just a comment. The same week (!) when Dylan asked this question, we received at our department a message from a non-professional mathematician who wrote a computer program that tries to simplify knots using level moves. (A "level move" is like an under move, but there can be more strands lying below the arc that you move.) He says that he tried all unknots he could find on the web and they can all be fully monotonically simplified in very little time (the crossing number strictly decreases at each step, as far as I see).

For instance, the Gordian knot (shown below) can be fully monotonically simplified using level moves.


Gordian

His program produces nice understandable pictures, and looking at them you can easily follow the moves that unknot the knot. These are available here

He actually wrote to us to ask for more examples to test the program with (there are not so many ready-to-use examples around), so if you know more hard unknots please share them (here or somewhere else)

Glorfindel
  • 2,743
Bruno Martelli
  • 10,164
  • 2
  • 37
  • 69
  • What happens when you run this program on a heavily twisted version of non-trivial knot, something like (Gordian unknot)#Trefoil? Does the program monotonically decrease the crossing number until you get to a more or less canonical representation of the knot? – Michael Nov 04 '14 at 17:08
  • I don't know (I still haven't seen the program running), but if you perform the diagram connected sum I suppose it simplifies the knot exactly as before. One should try some hard version of the trefoil knot... – Bruno Martelli Nov 04 '14 at 19:43
  • 1
    Things that are obvious to humans are not necessarily obvious to computers, so there is a possibility for a connected sum to get tangled. However, you are right, that would be a too easy a test. How about this one: consider the usual embedding of a torus in $R^3$ and let the trefoil (or any torus knot) run over that torus as usual. Then take that torus and tangle it into the thick version of the Gordian unknot. That would lead to a seriously tangled trefoil. – Michael Nov 04 '14 at 21:23
  • That's pretty nice, thanks for the pointer. The program looks pretty effective, and I'm curious what it does on that satellite trefoil. – Dylan Thurston Nov 05 '14 at 15:53
11

I recall a discussion on this question on math.sci.research quite a few years ago. John Conway had tried various moves to supplement Reidemeister moves. If I recall correctly, his guess was that no finite collection of moves will give monotonic simplification.

The Goeritz unknot below admits a simplifying move along the dashed arc shown. If one takes its untwisted double (as Ryan suggested) one again gets an unknot. (I hope I got the twists right below, but if not then adding twists shouldn't hurt). I don't see any obvious simplifying moves, or even any helpful lateral moves, for the bottom diagram.

Added: Marco correctly points out that while the doubling construction destroys the simplification at top left, it does not kill the one at bottom right. There is nothing to stop one from doing an additional untwisted doubling, with the clasp put at lower right. Perhaps that will do the trick.

Untwisted double of a Goeritzd unknot

Joel Hass
  • 871
  • 3
    I think there's a simplifying move, and I'll try my best to describe it. Take the inner strand running along the right-hand, bottom-most corner, and drag it below the three crossings on the right. This should eliminate two crossings while gaining only one (with the "twin" strand). – Marco Golla Nov 28 '14 at 15:47
  • You can do some level moves to move the clasp around, then do the over or under move that was there before. – Dylan Thurston Nov 30 '14 at 05:05
  • 1
    As suggested by Marco, this knot can be fully simplified via level moves, see http://www.zanellati.it/knot/Satellite_knot.pdf I just got this information from the author of the program who is following this page, so drawings of more complicated unknots are welcome :-) It would be interesting to try one more additional doubling as suggested by Joel... – Bruno Martelli Dec 03 '14 at 17:09
  • I found the comment by Conway related to this question at: https://groups.google.com/forum/print/msg/geometry.research/qsVMnaoCa9c/FcWkhqXEsnIJ?ctz=3250104_76_76_104100_72_446760 – Joel Hass Mar 07 '16 at 00:25