Inside-out polygonal dissections

Question

A dissection of a polygon $P$ is a partition of $P$ into a finite number of pieces, which can then be rearranged (via planar translations and rotations) and joined (without overlap) to form a new polygon $P'$. Say that a polygon $P$ has an inside-out dissection (my terminology) if $P'$ is congruent to $P$, and the perimeter of $P$ becomes interior to $P'$, and so the perimeter of $P'$ is composed of internal cuts of the dissection of $P$.

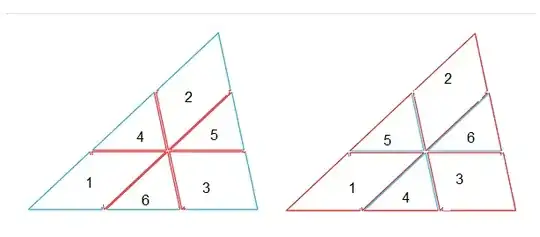
I believe every polygon $P$ has an inside-out dissection because (1) $P$ may be triangulated, and (2) every triangle has an inside-out dissection:

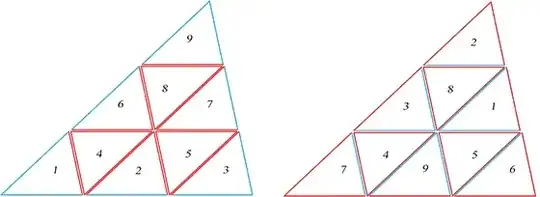
One may ask many questions concerning this concept. Here I will confine myself to three:

Q0. Has this notion been explored before, and if so, under what name?

Q1. Is there an inside-out dissection of a generic triangle using fewer than $9$ pieces?

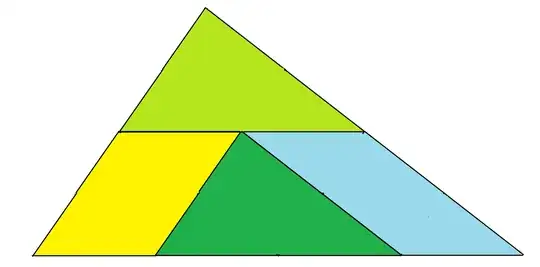
Q2. There is a "$+$" inside-out dissection of any rectangle into $4$ pieces. What is the minimal inside-out dissection of a generic trapezoid?

For acute triangles, 7 comes to mind (2 isosceles triangles at each vertex). — The Masked Avenger, Nov 06 '14 at 00:47
It also works for arbitrary polygons (2n+1) if the triangles are skinny enough. — The Masked Avenger, Nov 06 '14 at 00:51
For a trapezoid, bisect it and unfold it to a parallelogram half the height. Clip a piece off one end of the pgram and translate it to the other end. Clip the longest of the three pieces in such a way as to fold up into a similar trapezoid. For many trapezoids, this is a four piece dissection. — The Masked Avenger, Nov 06 '14 at 00:59
Are you excluding vertices of the dissection that lie on the boundary of both $P$ and $P^\prime$? — Michael Biro, Nov 06 '14 at 01:41
@MichaelBiro: Yes, Michael; I should have made that clear. Thanks for pointing that out. — Joseph O'Rourke, Nov 06 '14 at 01:47
This reminds me of hinged dissections. http://arxiv.org/abs/0712.2094 The classic hinged dissection of a square into an equilateral triangle is also an inside-out dissection, though not all hinged dissections are. Question: Does the Abbott et al. construction of hinged dissections yield an inside-out dissection? If not, can their result be strengthened to give a dissection that is simultaneously hinged and inside-out? — Timothy Chow, Nov 06 '14 at 16:30
@TimothyChow: Nice questions, especially in light of David Eppstein's mirror dissections, which are hinged. — Joseph O'Rourke, Nov 06 '14 at 16:32
Another thought: Aaron's dissection, and the square/triangle hinged dissection I mentioned above, are what you might call "perfect": Every edge of every component shape appears in the perimeter of exactly one of the two large shapes. Question: When is a perfect inside-out dissection possible? — Timothy Chow, Nov 07 '14 at 00:09
@TimothyChow: Clever riff! My own 9-piece dissection, and Aaron's 6-piece dissection, are not perfect. But the TMA's modification illustrated below is perfect---all-red cuts interior to all-blue edges interior. Perhaps this should be called pluperfect, for it is stricter than your exactly-one criterion? For polygons in general, identifying perfect inside-out dissections seem challenging. You've opened new territory with your questions! — Joseph O'Rourke, Nov 07 '14 at 01:05
Joseph, given that we're talking about inside-out dissections, there is no distinction between perfect and pluperfect, right? — Timothy Chow, Nov 07 '14 at 16:38
consider doing an inside-out dissection of a polygon such that the total length of cuts is minimized. As shown below, for any triangle T, there is an inside out dissection with total cut length = half the perimeter of T itself - a 'perfect' dissection. Likewise for rectangles or regular hexagons.
Which polygon P gives an upper bound on the length of cuts (compared to perimeter of P) for an inside out dissection?

How will such an upper bound change if we allow P' to be non-congruent to P - insisting only that the perimeter of P becomes interior to P'? — Nandakumar R, Mar 26 '20 at 15:21
Please note: in above comment, "as shown below" means, "as shown below on this page". And let us assume the input polygon P to be convex. Some thoughts on the above comment have been recorded at https://nandacumar.blogspot.com/2020/03/on-inside-out-dissections-of-polygons.html — Nandakumar R, Mar 26 '20 at 21:19

Aaron Meyerowitz · Accepted Answer · 2014-11-06T05:07:58.323

8

Your triangle dissection into $9$ pieces can be modified: enter image description here .

As masterfully noted below, The dissection into $16$ congruent triangles similar to the big triangle can be fused into four pieces. Swap the two triangles and rotate each parallelogram $180^{\circ}.$

enter image description here

edited Nov 06 '14 at 05:07

answered Nov 06 '14 at 02:13

Aaron Meyerowitz

30,015

3

You can do a 4 piece variation that gets rid of pieces 4 and 5, turns 2 and 6 into congruent triangles, and leaves 1 and 3 as parallelograms. – The Masked Avenger Nov 06 '14 at 02:35
1

More generally, take a polygon which tiles the plane without reflection. Offsetting this tiling by a carefully chosen epsilon vector should yield an inside out decomposition. – The Masked Avenger Nov 06 '14 at 02:55
Brilliant! Surely 4 is the minimum for triangles. – Joseph O'Rourke Nov 06 '14 at 12:53

score 5 · Answer 2 · answered Nov 06 '14 at 06:43

5

Do you allow mirror reflection to count as congruent? Because my paper Hinged Kite Mirror Dissection (arXiv preprint, 2001) dissects and reassembles an arbitrary polygon to become its mirror image; all exterior edges of the original polygon become interior edges of the dissection. So this is sort of an answer to Q0. Additionally (unlike your triangulation argument) the dissection is hinged. But the paper doesn't explicitly talk about your inside-out property.

answered Nov 06 '14 at 06:43

David Eppstein

18,497

Nice, David! I was retricting myself to rotations and translations, so was excluding mirrors as congruent. I had forgotten about your paper. – Joseph O'Rourke Nov 06 '14 at 10:43

score 2 · Answer 3 · answered Nov 06 '14 at 03:13

Riffing off the tiling comment to another answer, imagine a square penny packing of circles, and then translate the tiling so that a circle is in the center of four other circles. Now replace each of the five circles with a translate of a sufficiently convex (but not necessarily regular!) polygon, and you will for some polygons get a five piece inside out dissection.

score 1 · Answer 4 · answered Nov 06 '14 at 12:51

1

Here is another view of the @AaronMeyerowitz / @TheMaskedAvenger 4-piece inside-out dissection of a triangle:

answered Nov 06 '14 at 12:51

Joseph O'Rourke

149,182
34
342
933

1

Note that the parallelograms do not need to have tha same area. A follow up question: which polygons have such a three piece dkssection? I have only one candidate so far. – The Masked Avenger Nov 06 '14 at 15:08
1

Since no one else has remarked on this aspect, I do so: this is not only a hinged dissection, this is a special case of a hinged trapezoidal dissection, answering Q2 of the original post. (I believe 3 pieces does not hide all of the trapezoids corners.) – The Masked Avenger Nov 08 '14 at 18:35

Inside-out polygonal dissections

4 Answers4

Linked