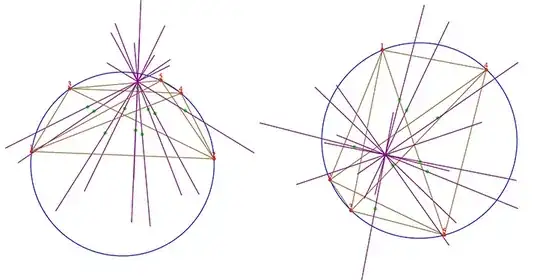
Your solution takes two lines, calculates their intersection, and confirms that it is as you claimed. Here is a proof which uses position vectors to show that each line goes through the specified point $$\mathbf{p}=\frac{\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d}+\mathbf{e}}{3}.$$ I note at the end that this proof works as well if their are more points (with a slight change) and also in $3$ or more dimensions. The proof certainly works, but I still am not satisfied that it is as clear as it could be.
update I have a more direct proof (at the end) of an even more general result. Unfortunately, as sometimes happens, as the proof improves, the initially surprising result seems less amazing.
The claim is that, given 5 points $\mathbf{a},\mathbf{b},\mathbf{c},\mathbf{d},\mathbf{e}$ on a circle $\mathbf{x} \cdot \mathbf{x}=r^2$ (i.e. centered at the origin), the line through the point $\mathbf{p}$ and the centroid $$\mathbf{q}=\frac{\mathbf{a}+\mathbf{b}+\mathbf{c}}3$$ of the triangle determined by the first three is perpendicular to the line through the points $\mathbf{d}$ and $\mathbf{e}.$ The first line, $\overline{\mathbf{pq}},$ is in the direction of the vector $\mathbf{d}+\mathbf{e}$ and the second line, $\overline{\mathbf{de}},$ is in the direction of the vector $\mathbf{d}-\mathbf{e}.$ The dot product of these two direction vectors is $\mathbf{d}\cdot \mathbf{d}-\mathbf{e}\cdot \mathbf{e}=r^2-r^2=0.$ Hence they are, indeed, perpendicular.
Generalization:
Given $n+2$ points $\mathbf{a_1},\mathbf{a_2},\cdots,\mathbf{a_{n+2}},$all equally distant from the origin, consider all $\binom{n+2}{2}$ lines determined by choosing $n$ of the points and taking the line through their centroid which intersects and is perpendicular to the line determined by the other $2.$ These lines all pass through the point $$\frac{\mathbf{a_1}+\mathbf{a_2}+\cdots+\mathbf{a_{n+2}}}{n}$$.
update Another proof.
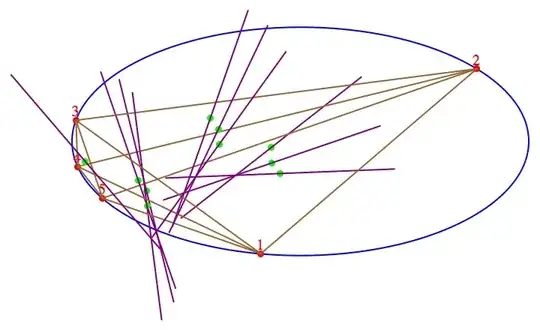
The detail I was missing is that the direction perpendicular to a cord $\overline{\mathbf{de}}$ of a circle is the one from the center of the circle to the centroid $\frac{\mathbf{d}+\mathbf{e}}{2}$ of the cord. Or simply from the center to $\mathbf{d}+\mathbf{e}.$ If we specify the direction in this way we no longer need to mention/require a circle.
Given given 5 points $\mathbf{a},\mathbf{b},\mathbf{c},\mathbf{d},\mathbf{e},$ take the line through the centroid of the triangle determined by some three which is in the direction of the sum of the other two. There are ten ways to do this. CLAIM: all ten meet at a common point.
Proof: one way is the line through the point $$\mathbf{q}=\frac13(\mathbf{a}+\mathbf{b}+\mathbf{c})$$ in the direction of the vector $\mathbf{d}+\mathbf{e}.$ The general point on this line has the form $$\mathbf{q}+t(\mathbf{d}+\mathbf{e})=\frac13(\mathbf{a}+\mathbf{b}+\mathbf{c})+t(\mathbf{d}+\mathbf{e}).$$ The other $9$ lines are similar with some other partition of the $5$ points. Clearly, the choice $t=\frac13$ shows that the point $$\mathbf{p}=\frac{\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d}+\mathbf{e}}{3}$$ is on all $10$ lines.
We could scale up by a factor of $3$ and replace the centroid by the sum of the vertices: The line through the sum of some three, say $\mathbf{a}+\mathbf{b}+\mathbf{c}$, in the direction of the sum of the other two $\mathbf{d}+\mathbf{e}$, passes through the sum of all five.
Theorem: Consider any $N=n+m$ points $\mathbf{a}_1,\mathbf{a}_2,\cdots ,\mathbf{a}_N.$ Consider all $\binom{N}{m}$ lines determined by splitting them into disjoint groups of size $n$ and $m$, taking the centroid $\mathbf{q}$ of the first group and the line through it in the direction of the vector from the origin to the centroid (equivalently, sum) of the second group. Then all these lines are concurrent at the point $$\frac{\mathbf{a_1}+\mathbf{a_2}+\cdots+\mathbf{a_{N}}}{n}.$$
If we scale up by $n$ and replace the centroid by the sum, then the point of concurrence is just $${\mathbf{a_1}+\mathbf{a_2}+\cdots+\mathbf{a_{N}}}.$$
We might need to rule out, or specify what to do, in uninteresting degenerate cases such as when a centroid is at the origin.