2

Let $(N \subset M)$ be an irreducible finite index subfactor.

If its lattice of intermediate subfactors is equivalent to $B_3$ (the lattice of divisors of $n=p_1p_2p_3$ square free):

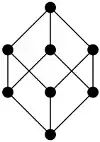
enter image description here

Question: Is there $p \in P_{2,+}(N \subset M)$ minimal central projection, generating the identity biprojection?

Notation: The biprojection generated by a projection $p$ is the smallest biprojection $b \ge p$.
The identity biprojection is the Jones projection $e_M$.

Remark: $B_3$ is distributive and the answer is yes for all the distributive lattices if the biprojection generated by a minimal central projection is always central; so it's true if $P_{2,+}(N \subset M)$ is abelian, for example the group-subgroup subfactors, and also for the depth $2$ case. It's also true if the lattice admits $<8$ vertices. $B_3$ is the smallest distributive lattice for which I don't know how to prove that in general.
In particular I don't know if it's true for the dual-group-subgroup subfactors $(R^G \subset R^H)$, but there is no counter-example for $B_3$ for $\vert G \vert \le 2000$ (except $512$, $768$, $1024$, $1280$).

Sebastien Palcoux
  • 25,922
  • In the group/subgroup case what group theoretical statement does this correspond to? – Noah Snyder Feb 08 '15 at 16:12
  • @NoahSnyder: if $(H \subset G)$ is an inclusion of finite groups, this corresponds to: $\exists g \in G$ such that $\langle H,g \rangle = G$ (see the proof here for all the distributive lattices). For the dual-group-subgroup case, the group theoretical statement is more complicated, it is explained here. – Sebastien Palcoux Feb 08 '15 at 17:00

1 Answers1

1

Yes, there is a proof for $B_n$ with $n \le 4$ in this paper (Corollary 6.12 p29).

Sebastien Palcoux
  • 25,922