What's the detailed proof of "the composition of planar tangles is well-defined"?

Question

In the planar algebra theory (see here or there section 2), a planar tangle is an isotopy class; then to define the composition of two tangles, we need to choose a representative in each classes. See below for a quick definition of planar tangles, composition and tangle isotopy.

Question: What's the detailed proof of "the composition of planar tangles is well-defined"?
(with all i's dotted and t's crossed)

Remark: A series of lectures given by Vijay Kodiyalam on the fundation of the planar algebra theory can be found in this link.

Quick definition of planar tangles and composition

A (shaded) planar tangle is the data of finitely many "input" disks, one "output" disk, non-intersecting (smooth) strings giving $2n$ intervals per disk and one $\star$-marked interval per disk. A tangle is defined up to isotopy.

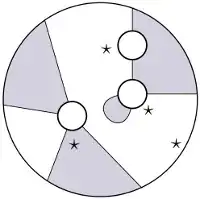
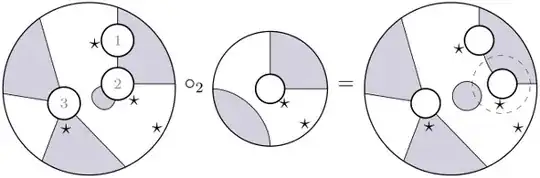
enter image description here

To compose two planar tangles, put the outup disk of one into an input of the other, having as many intervals, same shading of marked intervals and such that the marked intervals coincide. Finally we remove the coinciding circles (possibly zero, one or several compositions).

enter image description here

Tangle isotopy

The definition of a tangle isotopy is implicitly the one so that the "data needed" (for subfactors theory) is kept.
I will try an explicit and concrete definition (I invite the experts to correct it).

Two tangles are isotopic if we can go from one to the other by the following smooth deformation:

the radius and the center of an "input" disk can smoothly vary as long as the radius stays strictly positive and as long as the "input" disk does not touch an other "input" disk, an other string or the border of the "output" disk.
the contact points of a disk (with strings) can vary smoothly as long as they don't cross (or touch) themselves.
when an "inner" disk varies or when the contact points varies as above, an open strings touching the disk should vary smoothly so that the contact point follow the deformation, and the string does not touch itself, an other string, an other "input" disk or the border of the "output" disk.
a string can also vary smoothly as long as it keeps its endpoints (for the open string case), and as long as the string does not touch itself, an other string an other "input" disk or the border of the "output" disk.
the $\star$-marked intervals and the shading follow the deformation.
(optional) we could also add the "spherical isotopy" for the tangles whose "output" disk has no contact point.

To me the wikipedia's definition of planar algebra is unreadable, just horrible. — Włodzimierz Holsztyński, May 26 '15 at 16:16
@WłodzimierzHolsztyński: the definition of planar algebra needs nice diagrams to become more clear, see for example this paper section 2. — Sebastien Palcoux, May 26 '15 at 16:24
It might help if you give your precise isotopy definition. Usually your isotopy equivalence relation would either keep the endpoints fixed, or at least keep them marked in some manner. You would either use the isotopy extension theorem or some theorem about diffeomorphisms of the boundary of a manifold extending over the interior to get your isotopy independence. That's the shape of a typical argument, but I haven't read the paper you link to so I don't know the precise definitions you would like to use. — Ryan Budney, May 26 '15 at 17:16
Something seems wrong. In your definition of a planar tangle, the boundary circles are not indexed or labelled. But when you compose, you are choosing an index (you see it in your $\circ_2$ notation). — Ryan Budney, May 27 '15 at 05:55
@RyanBudney: yes, this is because two tangles can admit zero, one or several compositions. In this example there is only one input disk coinciding with the output disk of the other, but in general there could have zero, one or several allowed choices. So more precisely, the question should be: for a given allowed choice, why the composition is well-defined? Note that I'm not the designer of these diagrams, they come from this paper section 2. — Sebastien Palcoux, May 27 '15 at 06:15
With the labels you have just enough information to make the gluing. The key fact is, up to isotopy, there is a unique orientation-preserving diffeomorphism of a circle. But this is not true for relative diffeomorphisms of pairs (circle, finite subset). Diffeomorphisms of such objects are determined by not just whether or not they preserve orientation, but also where one point in the finite set is sent. That's the purpose of your "star" label, to determine where one point goes. Does this help? — Ryan Budney, May 27 '15 at 15:24
@RyanBudney: I try to understand in what this help. Is this an argument for a complete proof or just a clue? Do you think that the proof is direct without any problem? — Sebastien Palcoux, May 27 '15 at 16:10
Well in a sense we are dancing around a complete proof, but in part that's because the definition tries to avoid the technical issues at the heart of the problem. I think if you go through the argument that the group of isotopy-classes of diffeomorphisms of a pair $(S^1,F)$ where $F \subset S^1$ is finite, that this group is a dihedral group for an $n$-gon where $F$ has $n$ elements, once you see this proof you will likely see how it completes the proof you are looking for. — Ryan Budney, May 27 '15 at 16:31
@RyanBudney: Is there a way to describe the tangle isotopy much more briefly? — Sebastien Palcoux, May 29 '15 at 11:02
I'm kind of swamped reconstructing my house at present so I'm not logging in very much (let alone talking math with other human beings often). But I'd be happy to go into more details in one-on-one conversations. — Ryan Budney, Jun 17 '15 at 04:26

Stephen Bigelow · Accepted Answer · 2016-07-16T02:19:36.213

You could define the composition of planar tangles in a way that is obviously well-defined. Something like:

Scale the input planar tangle to half the size of the hole it goes in. Rotate the input disk so the two stars are on the same radial line. Finally, connect endpoints using the unique arcs that are linear functions in polar coordinates and do not cross the radial line between the two stars.

EDIT: On second thoughts, that did not address your question, since I still implicitly chose a representative input disk from the equivalence class. Let me try again.

If I understand right, your definition of composition is: choose a representative input tangle such that the endpoints and marked regions match up correctly, and then insert it into the input disk. And your question is: prove that if two tangles both match up correctly and are isotopic to each other, then inserting them into the input disk gives isotopic tangles. Is that right?

You could use:

Lemma: If two homeomorphisms $f,g:D \to D$ are isotopic and agree on a finite set of points then they are isotopic relative to that finite set of points.

If two input tangles are isotopic relative to the endpoints on the boundary, then it's easy to extend that isotopy to the larger tangle.

Sorry I haven't dotted my i's and crossed my t's, but I think it would be straightforward (though tedious) to turn this into a rigorous proof.

Hi Stephen. FYI you can edit your answer and amalgamate your two replies into one. It appears as if you used the same user account for the two replies, so this feature should be available. "edit" appears on a line immediately below your reply, and above this comment. — Ryan Budney, Jul 12 '16 at 07:29

What's the detailed proof of "the composition of planar tangles is well-defined"?

1 Answers1

Linked