This suggests a variant on Polya's orchard problem. That problem asks1 for which radius $\epsilon$ of trees at each lattice point within a distance $R$ of the origin block all lines of sight to the exterior of the orchard. It was established in the 1980's that rays to infinity are completely blocked iff $\epsilon \ge 1/\sqrt{R^2 + 1}$, when $R$ is an integer.2 E.g., for $R=20$, $\epsilon = 1/\sqrt{401} \approx 0.05$ suffices.
The variant is: Only lattice points both of whose coordinates are prime numbers are fattened to $\epsilon$-trees, and the source of visibility is $(2,2)$ rather than $(0,0)$. For example, the below shows that $\epsilon=0.3$ is insufficient to block visibility for $R=20$:
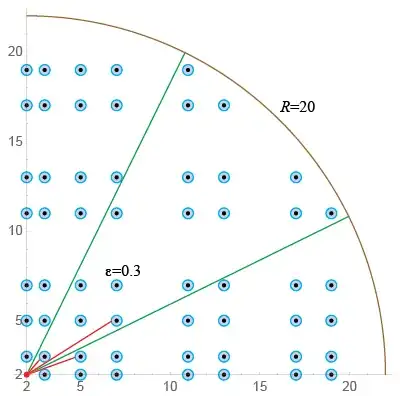
The basic question is:
Q1. For a given $R$, which $\epsilon$ suffices to block visibility from $(2,2)$ to beyond $R$ ?
As this does not seem easy to answer precisely, let me pose a very specific question:
Q2. As $R \to \infty$, does $\epsilon \to 0$?
It could be that the thinning of the prime trees is rapid enough to require some lower bound on $\epsilon$ to block visibility, even for large $R$.
1Here I am quoting from a previous MO question.
2Thomas T. Allen, "Polya's orchard problem." (Jstor link.) The American Mathematical Monthly 93(2): 98-104 (1986).)