37

What is the largest volume object that can pass though a $1 \times 1 \times L$ "snaky" corridor, where $L$ is large enough to be irrelvant, say $L > 6$.

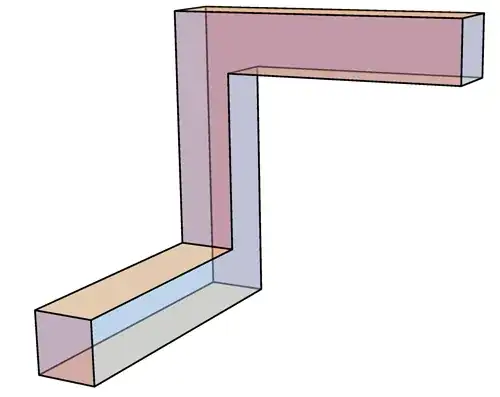
          SofaCorridor

This is a 3D version of the 2D sofa-moving problem, which has been heavily studied. See especially Dan Romik's web pages. The optimal-area 2D sofa is conjectured to be Gerver's (slight) modification of Hammersley's shape, the latter of which I show below, extruded in 3D to fill the corridor.

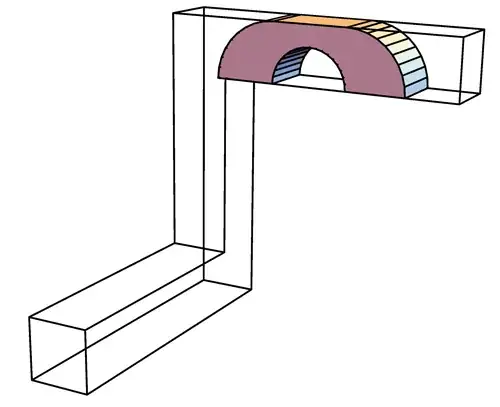
          SofaHammerslay
There are two natural candidates: (1) Slice the extruded 2D optimal shape, in the orthogonal direction, so it can negotiate both turns in the same manner. See image added below. (2) Rotate the illustrated shape $90^\circ$ but shear-off every portion that falls outside the $1 \times 1$ corridor.

A basic question is: Is either of these the optimal solution, or can one identify some shape that beats both? An even more basic (and easier) question is: Which of (1) or (2) has larger volume?

Added:

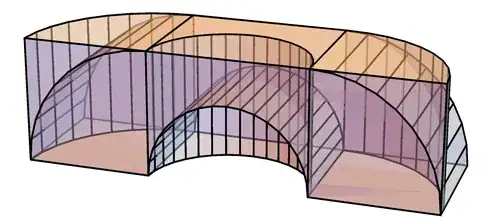
          Sofa90Carved
          The intersection of the two shapes can pass through the corridor.
          SofaCut
          The intersection. (Thanks to J.M. & JackLaVigne @MathematicaSE.)
Volume: $\frac{4 \left(8+\pi^3\right)}{3 \pi ^3} \approx 1.67735$.
Community
  • 1
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 1
    Maybe there is a way to make a simpler 3D-analog of the Sofa problem, with just one turning point, by requiring that one of the solid's axes must be aligned in some direction before and in some other direction after ? – F. C. Aug 06 '16 at 10:12
  • 1
    To rephrase my previous comment, contrary to the plane case, the shape can arrive in its final position in 4 different ways. This gives 4 distinct problems. – F. C. Aug 06 '16 at 20:00
  • 1
    This is really off-topic but, what software did you use for the figures? – Sak Aug 07 '16 at 00:13
  • 1
    @Sak: Mathematica. – Joseph O'Rourke Aug 07 '16 at 02:05
  • 9
    Also, what kind of building are you moving into? – Simon Rose Aug 16 '16 at 08:35
  • @SimonRose: An $n^\textrm{th}$ floor walkup. :-) – Joseph O'Rourke Aug 16 '16 at 11:30
  • 3
    The shape of egg may be connected with this problem. – Takahiro Waki Mar 23 '17 at 14:23
  • Could you explain your calculations here? I am doing similar calculations and finding a different area. –  Apr 15 '17 at 20:15
  • or rather volume. –  Apr 15 '17 at 20:39
  • @Benjamin: I used Mathematica's RegionMeasure[] function. I will have to go back to my calculations to see how I arrived at that expression. – Joseph O'Rourke Apr 15 '17 at 20:54
  • 1
    @JosephO'Rourke Nevermind, I found an error in my calculations. –  Apr 17 '17 at 19:28
  • Is it clear that the extruded version of the best shape in the 2 dimensional case is the best in the 3-dimensional case for passing the first part? – Gerardo Arizmendi Jun 13 '17 at 17:18
  • @GerardoArizmendi: Definitely not clear. Just a lowerbound on the volume of the optimal shape. – Joseph O'Rourke Jun 13 '17 at 17:26
  • 1
    @Sak, It's not the camera, it's the photographer. :-) – Michael Feb 22 '19 at 16:32
  • 2
    Another natural 3D variant of the question would be a pipe with circular rather than square cross-section and bends allowed in arbitrary direction. One can also ask questions regarding what the maximality of the body's volume implies about the body's symmetries: 1. For the pipe with square cross section and 4 bend direction must the maximal body have D_8 symmetry? 2. For the pipe with circular cross-section and arbitrary bend direction must the body have O(2) symmetry? – Michael Feb 22 '19 at 16:42
  • Even the single-bend version of this problem might be interestingly different from the 2D sofa problem - perhaps the ability to turn on a new axis when passing through the corridor allows for solutions that don't consist of the product of a flat surface with an interval. – RavenclawPrefect Oct 09 '22 at 21:36
  • I love this kind of problem: Only crazy mathematicians put sofas into snakes! – Roland Bacher Oct 10 '22 at 08:12

1 Answers1

2

[Not a solution, just answering the "even more basic" question of the original post.]

The Hammersley sofa is given by cutting a semicircle of radius $2/\pi$ out of a $1\times 2/\pi$ rectangle and adding unit-radius quarter discs to the sides:

This sofa has area $\frac{\pi}2+\frac2\pi-\frac2{\pi^2}=2.2017$, so of course its 3D variant extruded by a distance of $1$ in the $z$-axis has the same volume.

If we intersect this sofa with a cylinder of radius $0.5$ positioned within the corridor (i.e. $(x-0.5)^2+(z-0.5)^2\le0.25$), the resulting shape will be able to rotate after making the first turn, so that it will be in position for the second turn. The volume of this rounded shape is given by

$$\int_0^12\sqrt{0.25-(y-0.5)^2} \left(\frac2\pi+2\sqrt{1-y^2}\right)\,dy $$ $$- \int_0^{2/\pi}2\sqrt{0.25-(y-0.5)^2}\cdot2\sqrt{\frac4{\pi^2}-y^2}\,dy$$ $$\approx1.76755 > 1.67735$$

so it is an improvement over the intersection with a $90$-degree rotated copy. (One could probably improve slightly on this by performing the same operation to Gerver's improved sofa, but the exact integral becomes much more ugly.)

One could try intersecting with other square rotors, like a Reuleaux triangle at various orientations:

                                          enter image description here

Empirically this didn't seem to improve things, as might be expected from the fact that the Releaux triangle is the minimal-area square rotor. Area isn't the only consideration here though, since the weighted sum of the widths of our rotor at different heights is what matters.

RavenclawPrefect
  • 2,298