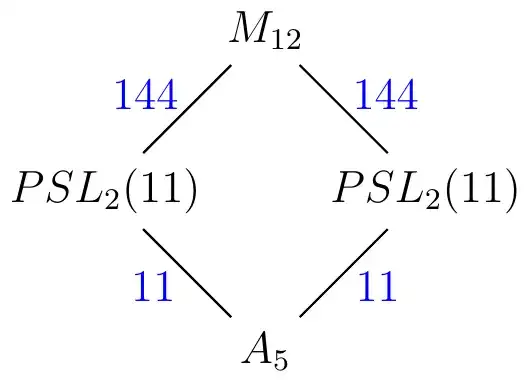
Let $[H,G]$ be a rank $2$ boolean interval of finite groups.
Statement 1: There is an atom $K$ of $[H,G]$ such that $|K:H|≡|G:H|($mod $ 2)$.
The following picture illustrates the statement.

Question: Is it true?
It is true in each of the following cases:
- $|G:H| = 2p$ with $p$ prime (see below)
- $|G:H|<36$ (using GAP and $34=2 \cdot 17$)
- $G$ simple with $|G| \le 50000$ (by GAP)
For $|G:H| = 2p$ the proof is the following: if $|G:K_i| = 2$ then $K_i$ is a normal subgroup of $G$. It follows that $H=K_1 \cap K_2$ is also normal so $[1,G/H] \simeq [H,G]$ boolean, so by Ore's theorem $G/L$ is cyclic, but with two subgroups of index $2$, contradiction.
Application: Assuming Statement 1 true, we can prove the following:
Statement 2: Let $[H,G]$ be a boolean interval of rank $>1$, then there is a coatom $L$ of $[H,G]$ with $|L:H|≡|G:H|($mod $ 2)$.
Proof: if $|G:H|$ is odd, it is immediate, so we can assume that $|G:H|$ is even. If for every coatom $L$, $|L:H|$ is odd, take two coatoms $L_1$ and $L_2$, then $[L_1 \wedge L_2,G]$ is a rank $2$ boolean interval which contradicts Statement 1. $\square$
Statement 3: Let $[H,G]$ boolean, then there is an atom $K$ with $|K:H|≡|G:H|($mod $ 2)$.
Proof: Idem we can assume that $|G:H|$ is even. We prove by induction on the rank of $[H,G]$. It is immediate at rank $1$. Assume it is true at rank $<n$. For $[H,G]$ of rank $n$, by Statement 2, there is a coatom $L$ with $|L:H|$ even, but $[H,L]$ is a rank $n-1$, the result follows. $\square$
Note that Statement 3 implies Statement 1, so all these statements are equivalent.