10

It is a theorem of Masur that all rational triangles in the Euclidean plane posses a periodic billiard path, one obeying the reflection law that the angle of incidence equals the angle of reflection. A rational triangle has angles that are rational multiples of $\pi$. It remains an open question of whether all triangles have a periodic billiard path.

Q. Is there some analogous theorem for hyperbolic triangles in the hyperbolic plane?

A billiard path in a hyperbolic triangle consists of geodesics which reflect from the sides of the triangle by the same reflection law. Here is a possible start of a billiard path inside a triangle drawn in the Poincare half-plane model, where the geodesics are circular arcs and vertical line segments:

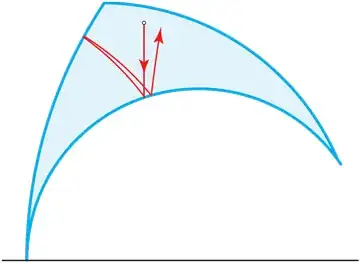
          HyperbolicTri
Is there some analog of the Euclidean rational angle condition that yields a theorem for hyperbolic triangles?
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 3
    Consider one parameter family of hyperbolic triangles such that the angles decrease. It seems that if at the beginning you had a closed orbit then it survives in the family (?). If this is true then you may start with any Euclidean triangle for which you know that a trajectory exists and get a trajectory for any hyperbolic triangle with smaller angles. It seems that the set of Euclidean triangles with periodic trajectories is dense therefore all hyperbolic triangles have to have a periodic trajectory. – Anton Petrunin Sep 20 '16 at 00:31
  • @AntonPetrunin: "all hyperbolic triangles have to have a periodic trajectory": Remarkable! – Joseph O'Rourke Sep 20 '16 at 00:46
  • 2
    The review of Alfonso Artigue, Expansive flows of the three-sphere, Differential Geom. Appl. 41 (2015) 91-101, MR3353741 refers to "the billiard in a geodesic triangle in the hyperbolic disc", so it might be good to have a look there. – Gerry Myerson Sep 20 '16 at 02:56
  • 3
    @AntonPetrunin Why do you believe the sentence you have marked with a (?)? (Also, shouldn't the orthic triangle work for all acute hyperbolic triangles?) – Neal Sep 20 '16 at 03:24
  • 2
    This is only a wild guess, but my suspicion is that billiards in hyperbolic triangles are chaotic in the sense of Devaney and should have infinitely many periodic orbits irrespective of their angles. – Ian Morris Sep 20 '16 at 09:45
  • @GerryMyerson: One quote from the reference you cite: "the billiard map of a triangle on the hyperbolic disk has non-vanishing Lyapunov exponents." However, I am uncertain of the consequences of this fact. – Joseph O'Rourke Sep 20 '16 at 11:33
  • 2
    Theorem 3 of "Expansive billiard flows" (arxiv.org/pdf/1207.3116) asserts that a billiard flow in a polygonal subset of the Poincare disc has a dense set of periodic orbits, but this paper seems to be unpublished and uncited. – Ian Morris Sep 20 '16 at 12:14
  • 3
    @Neal: I can't speak for Anton Petrunin, but take a periodic orbit in a Euclidean triangle and consider its combinatorics (the word of the successively sides it hits, up to circular permutation) ; I would guess that this orbit is a (at least local) length minimizer in the class of closed curves that touch the boundary with the same combinatorics. Then a very small hyperbolic triangle close to that Euclidean triangle would have even better stability properties for the corresponding minimizing problem (it costs more to move a point across a vertex), and a minimizer must be a periodic orbit. – Benoît Kloeckner Sep 20 '16 at 12:29
  • At first, it should be about the case of spherical tringle. – Takahiro Waki Jan 03 '17 at 04:12

1 Answers1

4

If the triangle is a fundamental domain for a discrete group, a periodic orbit corresponds to a closed geodesic in the quotient surface, which gives you boat-loads of periodic orbits (to be precise, $\sim \exp(L)/L$ of them of length bounded above by $L.$ I think that if all the angles are rational, the triangle is a fundamental domain for a cone-metric, and while a lot of the closed geodesics will go through the vertices, an entropy computation (that is, the set of geodesics passing through the vertices have smaller entropy than the entire geodesic flow) will give you a similar result.

Igor Rivin
  • 95,560
  • I do not think entropy can feel it; did you made the calculations? – Anton Petrunin Sep 21 '16 at 01:08
  • @AntonPetrunin I have made similar computations a long while ago. Since the curvatures are all negative I am pretty sure this works... – Igor Rivin Sep 21 '16 at 08:07
  • 1
    You take the doubling of triangle and pass to its covering branching at the vertices, so that the curvature becomes negative. You claim that in the obtained space a random closed geodesic does not bump into vertex with probability near 1. Did I understood you correctly? If yes, then I am surprised and I need to think. – Anton Petrunin Sep 22 '16 at 01:55