3

Let $L$ be a finite lattice with $\hat{1}$ its maximum and $c_1, \dots, c_n$ its coatoms. Let $E_n=\{1, \dots, n \}$.
For any subset $I \subset E_n$ we define $$C(I) := \bigwedge_{i \in I} c_i$$ then let $$T:=C(E_n)$$ For any $a \in L$ we define $$I(a) := \{i \in E_n \mid a \le c_i \}$$ and $$ R(a) := C(I(a))$$ Let $a \in L \setminus [T,\hat{1}]$ and $b \in [T,\hat{1}]$ such that $a < b$. Then $R(a),b \in [a,R(b)]$, obviously.

Question: Is it true that $R(a) \le b$ if $L$ is modular?

Remark: It is true if $L$ is distributive because then $[T,\hat{1}]$ is boolean, so that $b = R(b)$.

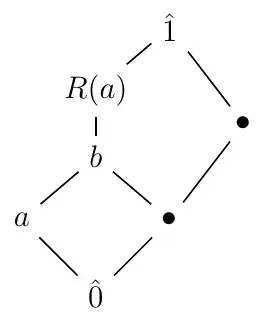
Remark: If we don't assume $L$ modular, then it is false, as for the following lattice with a pentagon: enter image description here

Community
  • 1
Sebastien Palcoux
  • 25,922

1 Answers1

5

Question: Is it true that $R(a)\leq b$ if $L$ is modular?

Yes. In a modular lattice of finite length, if the coatoms meet to zero, then the lattice is relatively complemented. This fact applies to the interval $[T,\hat{1}]$, and it entails that any element in this interval is a meet of coatoms. Thus, $R(b)=b$ for every $b$ in $[T,\hat{1}]$. Since the $R$-map is order-preserving, $R(a)\leq R(b) = b$.

Keith Kearnes
  • 12,143
  • About any of the following two implications of your answer: << (...) then the lattice is relatively complemented. >> and << (...) it entails that (...) >>. Is it immediate, or an (easy) exercise, or a result requiring a reference? – Sebastien Palcoux Nov 12 '16 at 19:43
  • 2
    The second "it entails that" is immediate: the interval $[ T, \hat{1} ]$ is complemented, so the least element is the meet of coatoms. (Otherwise, the meet of all coatoms has no complement.) For the first, it is well-known that complemented and relatively complemented are equivalent in modular lattices. It is an exercise in e.g. Birkhoff that complemented is equivalent to $\hat{0}$ being a meet of coatoms in semimodular lattices. – Russ Woodroofe Nov 12 '16 at 19:54
  • 2
    @RussWoodroofe: $T$ is the meet of all the coatoms of $L$ by definition. What you had in mind should be the following: $[T, \hat{1}]$ is relatively complemented, so for any $b \in [T,\hat{1}]$ then $[b,\hat{1}]$ is complemented, so $b$ is the meet of all the coatoms of $[b,\hat{1}]$. – Sebastien Palcoux Nov 12 '16 at 20:10
  • Let $R(b)$ be the meet of all the coatoms of $[b,\hat{1}]$ and let $a$ its complement in $[b,\hat{1}]$. If $a < \hat{1}$, then $a \le c_i , \ \forall i \in I(b)$. So by modularity, $$ \hat{1} = a \vee R(b) = a \vee (\bigwedge_{i \in I(b)}c_i) = \cdots = \bigwedge_{i \in I(b)}c_i.$$ Then $\hat{1} = R(b)$, contradiction. It follows that $a=\hat{1}$, and $R(b) = b$. – Sebastien Palcoux Nov 12 '16 at 20:51