Divisibility labeling on a boolean lattice and nonzero Euler totient

Question

Let $B_n$ be the subset lattice of $\{1,2, \dots , n \}$, also called the boolean lattice of rank $n$.
A labeling $f: B_n \to \mathbb{N}_{\ge 1}$ is called acceptable if $\forall a,b \in B_n$:

• $a < b \Rightarrow \frac{f(b)}{f(a)} \in \mathbb{N}_{\ge 2}$
• $ f(a)f(b) \le f(a \vee b)f(a \wedge b)$

Let $\varphi(f) := \sum_{a \in B_n} (-1)^{|a^{\complement}|}f(a)$ be the Euler totient of $f$.

Reminder (see this post and its answers): The divisor lattice of $m$ square-free is boolean of rank the number of prime factors of $m$ and $\varphi(f) = \varphi(m) > 0$. For $[H,G]$ boolean interval of finite groups, the labeling $f(K) = |K|$ is acceptable and $\varphi(f) > 0$ by Ore's theorem (for $G$ a Chevalley group and $H$ a Borel subgroup, $[H,G]$ is boolean of rank that of the Dynkin diagram of $G$). We know that at rank $\le 5$, $\varphi(f) > 0$ for any acceptable labeling $f$, but there are some at rank $6$ with $\varphi(f) < 0$.

Question: Is $\varphi(f)$ nonzero for any acceptable labeling $f$?

Motivation: A positive answer would give a purely combinatorial generalization of Ore's theorem.

Edit: We now request $a < b \Rightarrow \frac{f(b)}{f(a)} \in \mathbb{N}_{\ge 3}$, for two reasons:

• If there is an atom $K$ of $[H,G]$ boolean, such that $|K:H| = 2$, then $\forall T \in [H,K^{\complement}]$, $|T \vee K : T| = 2$, so that the Euler totient for $[H,G]$ equals the one for $[H,K^{\complement}]$.
• If we allow $\frac{f(b)}{f(a)}=2$, then there is a trivial infinite series of counter-examples: take $ m\ge 0$, then the $q$-deformation of the regular labeling (see the definitions in the accepted answer) for $$ r=2, \ s_1=2, \ n_1=2^{m+1}+4, \ s_2=2^{2^{m+1}+4+m}+1, \ n_2=1, \ q=2^m+1 $$ has rank $2^{m+1}+5$, and a zero Euler totient.

  ---

This question is related to tricky problems in modular arithmetic. We will give a series of non-trivial examples of acceptable labelings and prove that their Euler totient is nonzero:

Let $r,s,q \in \mathbb{N}_{\ge 2}$ with $r \wedge s = 1$. Consider the following labeling $f$ on $B_n$:
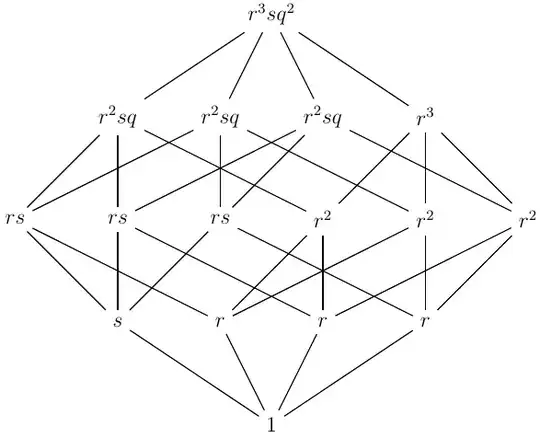
Take an atom $a$ of $B_n$, and label every maximal chain of $[\hat{0}, a^{\complement}]$ by $$(1, r, \dots, r^{n-1})$$ and every maximal chain of $[a,\hat{1}]$ by $$(s, rs, \dots, r^{n-3}s,r^{n-2}sq,r^{n-1}sq^2) $$

See below this labeling for $n=4$:

The labeling $f$ is obviously acceptable.

Proposition: The Euler totient $\varphi(f)$ is nonzero.
Proof: At rank $n+1$, we have $$\varphi(f) = s[(r-1)^{n}-(r^{n}-nr^{n-1})+(r^{n}q^2-nr^{n-1}q)]-(r-1)^{n}$$ $$= (s-1)(r-1)^{n} + sr^{n-1}(q-1)(r(q+1)-n)$$ So, $$\varphi(f) \equiv (s-1)(r-1)^{n} \mod r^{n-1}.$$ Now, assume that $\varphi(f) =0$, then $s\equiv 1 \mod r^{n-1}$, because $(r-1)\wedge r = 1$. So $s=k r^{n-1} + 1$ with $k \ge 1$. Then $$\varphi(f) = r^{n-1}[k(r-1)^{n} + (k r^{n-1} + 1)(q-1)(r(q+1)-n)]$$ Note that we must have $n < r(q+1)$ and $(r-1)^{n} > r^{n-1}$. It follows that $$3r+1 \le n \le \frac{ln(r-1)}{ln(1+\frac{1}{r-1})})$$ We deduce that $r \ge 24$ and $n \ge 73$, and also $n \le rln(r-1)$.

But $\varphi(f) =0$ implies that $$k(r-1)^{n} + (k r^{n-1} + 1)(q-1)(r(q+1)-n) \equiv (q-1)(r(q+1)-n) \equiv 0 \mod k$$ So there is $k'>0$ such that $(q-1)(r(q+1)-n) = -kk'$. It follows that $$\varphi(f) = r^{n-1}k[(r-1)^{n} - (k r^{n-1} + 1)k'] = 0$$ Then, $(r-1)^{n} = k'(k r^{n-1} + 1)$ and $k' \equiv (-1)^n \mod r$. So, $$(r-1)^{n} = (k''r+(-1)^n)(k r^{n-1} + 1)$$ with $k''\ge 0$. If $k'' \ge 1$, then $(r-1)^{n} \ge (r-1)(r^{n-1} + 1)>(r-1)^n$, contradiction. Then, $k'' = 0$, so $(-1)^n=1$, and $$(r-1)^{n} = k r^{n-1} + 1$$ So, it is necessary to have a solution for the following tricky equation

$$ (r-1)^{n} \equiv 1 \mod r^{n-1}$$

with $r \ge 24$ and $n \ge 3r+1 \ge 73$. By using arguments as in this answer, we deduce that:

• If $r \not \equiv 2 \mod 4$, then $2.2> \frac{2r}{r-2}>(1+\frac{1}{r-1})^n>(1+\frac{1}{r})^r>2.6$, contradiction.
• If $r \equiv 2 \mod 4$, then $m \ge r-2 = 2^mx \ge 2^m$ (with $x$ odd), contradiction.

It follows that $\varphi(f) \neq 0$. $\square$

Problem: Can we extend this proof to any acceptable labeling $f$?

Answer 1

No, we have found six primitive counter-examples at rank $11,14,15,15,20,28$, respectively.

Let $f_1$ and $f_2$ be two labeling on $B_{n_1}$ and $B_{n_2}$ respectively.
Let $f_1 \cdot f_2$ be a composition of $f_1$ and $f_2$, on $B_{n_1} \times B_{n_2} \simeq B_{n_1+n_2}$, defined by: $$ (f_1 \cdot f_2)(a_1,a_2) = f_1(a_1)f_2(a_2).$$ A labeling $f$ is primitive if it is not of the form $f_1 \cdot f_2$ (with $f_i$ non-trivial), and $f(\hat{0}) = 1$.
A composition of a labeling $f$ with itself $n$ times will be noted $f^n$.
Note that $\varphi(f_1 \cdot f_2)=\varphi(f_1)\varphi(f_2)$, and so $\varphi(f^n)=\varphi(f)^n$.

A labeling is called regular if $\forall a<b$ $$f(a)f(b) = f(a \vee b)f(a \wedge b)$$

Let $r>0$ and $3 \le s_1 < \cdots < s_r$ be integers.
Let $f_i$ be the labeling on $B_1$ defined by $f(\hat{0}) = 1$ and $f(\hat{1}) = s_i$.
Let $n_i>0$ be an integer and let $F$ be the labeling $f_1^{n_1} \cdot f_2^{n_2} \cdots f_r^{n_r}$, on $B_n=B_{n_1+\cdots +n_r}$.
Then, $\varphi(F)=\prod_{i=1}^r (s_i-1)^{n_i} > 0$. A labeling is regular iff it is of the form of $F$.

Let $q \ge 1$ be an integer and let $F_q$ be a $q$-deformation of $F$ defined by $F_q(\hat{1}) = q^2 F(\hat{1})$, $F_q(c) = q F(c)$ for any coatom $c$, and $F_q(a) = F(a)$ otherwise.

Note that the labeling $F_q$ is acceptable, and primitive if $q>1$. We compute that $$ \varphi(F_q) = \varphi(F) - (\prod_{i=1}^r s_i^{n_i-1}) \left[ \sum_{i=1}^rn_i\prod_{j \ne i}^r s_j - (q+1)\prod_{i=1}^r s_i \right] (q-1) $$ So $\varphi(F_q) = 0$ if and only if

$$\prod_{i=1}^r (s_i-1)^{n_i} = (\prod_{i=1}^r s_i^{n_i-1}) \left[ \sum_{i=1}^rn_i\prod_{j \ne i}^r s_j - (q+1)\prod_{i=1}^r s_i \right] (q-1)$$

Now this post is dedicated to the above equation, and this answer proves the following theorem:

Theorem: There are exactly six solutions with $3\le s_1 < \cdots < s_r \le 9$, given by

$$ \begin{array}{c|c} \prod_i s_i^{n_i} &3^{5}4^{5}9^{1} &3^{5}4^{1}6^{1}7^{4}8^{3} &4^{4}5^{6}6^{5} &3^{1}4^{8}7^{1}9^{5} &4^{7}5^{6}6^{5}9^{2} &3^{4}4^{3}5^{2}6^{1}7^{8}8^{7}9^{3} \newline \hline q &2&2&2&2&3&4 \newline \hline \sum_i n_i &11&14&15&15&20&28 \end{array}$$

We deduce the expected primitive and acceptable labelings whose Euler totients equal zero.

---

Question 1: What is the smallest possible rank for a counter-example?

It is easy to see that there is no counter-example with the model above at rank $\le 10$. But we can generalize the $q$-deformation as follows: take a (regular) labeling $F$ and let $F_{q,\ell}$ be the level $\ell$ $q$-deformation of $F$ defined by $F_{q,\ell}(a) = q^{\ell-|a^{\complement}|}F(a)$ if $|a^{\complement}| < \ell$, and $F_{q,\ell}(a) = F(a)$ otherwise. If $\ell=2$, we recover the previous deformation. By solving $\varphi(F_{q,\ell}) = 0$ for small values as above, we would find new counter-examples, and perhaps some at rank $\le 10$.

We can cook extra generalizations, for example, take $1 \le q_1 \le \dots \le q_{\ell}$, and define $F_{(q_1, \dots, q_{\ell})}$ by $$F_{(q_1, \dots, q_{\ell})}(a) = F(a)\prod_{i=1}^{\ell-|a^{\complement}|}q_i$$ if $|a^{\complement}| < \ell$, and $F_{q,\ell}(a) = F(a)$ otherwise. If $q_i=q$ for any $i$, we recover the previous deformation.

---

Let's call $f(\hat{1})/f(\hat{0})$ the index of the labeling.

Question 2: Is there a counter-example with odd index?

We have extended here the above theorem to $s_r \le 10$, there are $30$ solutions, none has odd index.