This impressive work was tested on ~60,000 models in the Protein Data Bank, computing the
volume of the union of sometimes more than 50,000 atoms represented as balls of different
radii. Implemented in C++:
Cazals, Frédéric, Harshad Kanhere, and Sébastien Loriot. "Computing the volume of a union of balls: A certified algorithm." ACM Transactions on Mathematical Software (TOMS) 38.1 (2011): 3. (ACM link.)
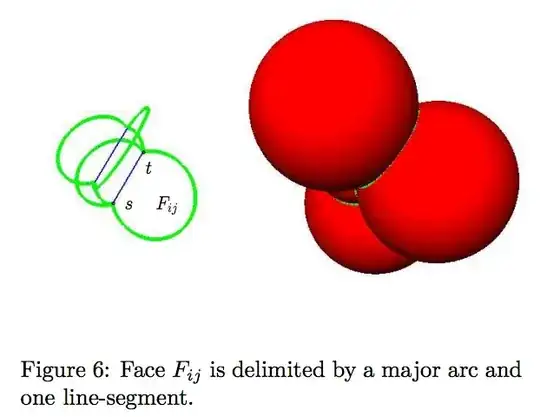
Their algorithm is based on the
"decomposition of the volume of the union into convex regions, namely the restrictions of the balls to their regions in the power diagram. Theoretically, we establish a formula for the volume of a restriction, based on Gauss' divergence theorem. The proof being constructive, we develop the associated algorithm."
