In his remarkable book On the Sphere and Cylinder, where he came tantalizingly close to discovering calculus, Archimedes showed that the area of the portion of the sphere contained between a pair of parallel planes cutting the surface depends only on the distance between the planes (see p. 625 of this paper of King). This fact, which has been dubbed Archimedes hatbox theorem, is now a standard exercise in many calculus texts, and is even commemorated on the back of the Fields medal (if you look closely there, you can see the figure below in the background).
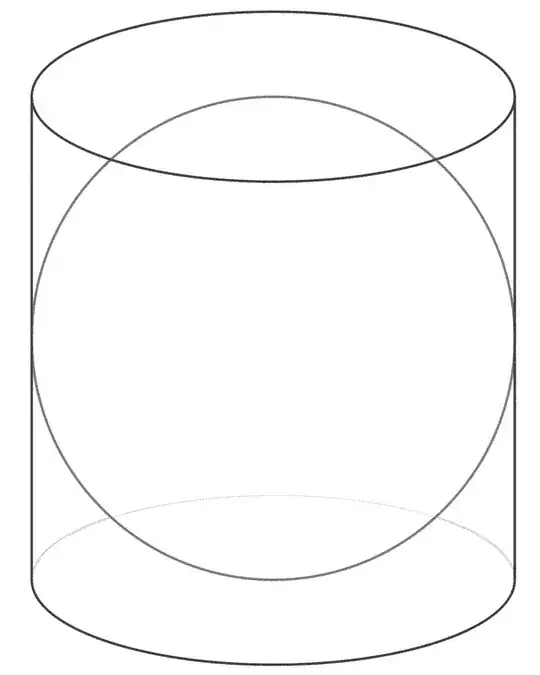
Conversely, Blaschke showed that the only convex surface with this slab area property is the sphere. Indeed it is a simple exercise in classical differential geometry to check that any smooth convex surface with the slab area property must have constant curvature (Let $A(h)$ be the area trapped between a tangent plane and a prallel plane at distance $h$, and compute the limit of $A(h)/h$ as $h\to 0$). But can one still characterize the sphere if we fix the distance between the planes:
Question: Let $S\subset R^3$ be a convex surface with diameter $d$. Suppose that for some constant $0<h<d$, the area of the portion of $S$ trapped between every pair of parallel planes separated by the distance $h$ is constant, whenever both planes intersect $S$. Does it follow then that $S$ is a sphere?
A convex surface is the boundary of a compact convex set with interior points, and its diameter is the distance between its farthest points in the ambient space. Although this is known to be an open problem, I am not aware if it has been explicitly mentioned anywhere.
Addendum: See this question for a closely related problem on plank invariant measures for convex planar's domains, and more references in this area.