18

Q. Is it possible to trap all the light from one point source by a finite collection of two-sided disjoint segment mirrors?

I posed this question in several forums before (e.g., here and in an earlier MO question), and it has remained unsolved. But I've recently become re-interested in it. Let me first clarify the question. It seems best to treat the mirrors as open segments (i.e., not including their endpoints), but insist that they are disjoint as closed segments. And the point source of light should be disjoint from the closed segments.

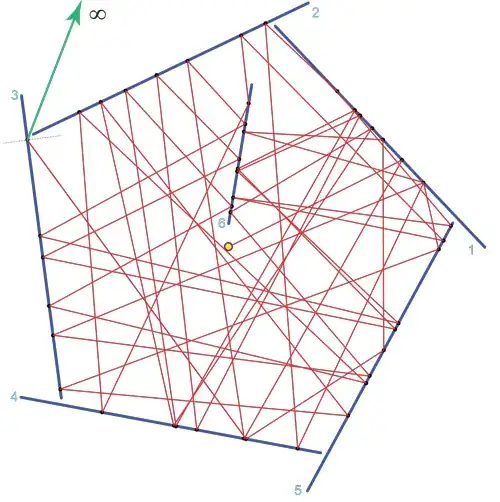
          Pent1
          $6$ mirrors. Lightray starts at center, exits (green) after $46$ reflections.
Of course a finite number of rays can be trapped periodically, and less obviously a finite number of rays can be trapped nonperiodically. But it seems quite impossible to trap all rays from a single fixed point. Because of segment disjointness, there are paths to $\infty$, and it seems likely that some ray will hew closely enough to some path to escape to $\infty$. So I believe the answer to my question is No.

Perhaps application of Poincaré recurrence could lead to a proof, but I cannot see it.

Related: Can we trap light in a polygonal room?.
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 2
    Interesting problem. First, in order to trap the light, all the "holes" through which the light could escape should be invisible from the source point. This rules out "simple" mirror configurations. I would think of the inverse problem. Consider a source of light in one of the "holes" near the exterior. The equivalent question is: is there any interior point which cannot be illuminated by a source in one of the holes – Beni Bogosel Nov 15 '17 at 16:02
  • 1
    This is more along the lines of Birkhoff's ergodic theorem, I think. If you have an open set (no matter how small) and an ergodic map (or flow), then almost every trajectory hits this open set (with the asymptotic frequency equal to the measure of the set). Of course, one needs to do this properly, probably using billiards (which I'm not an expert on). – Nikita Sidorov Nov 16 '17 at 11:13

0 Answers0