Wow. This deserves a separate answer.
As I mentioned in a comment, motivated by the question, in a previous comment, by Igor Rivin whether an efficient primality test can be made if the statement in the question is true, I asked a separate question about whether one could efficiently compute $T_n(x)$ modulo $x^r-1,n$. That question got a brilliant answer by Lucia, which enables to really demonstrate that if the statement in the question is true, one indeed obtains a very efficient primality test based on it.
I made this quick-and-dirty Mathematica code
polmul[f_, g_, r_, n_] := Mod[f.NestList[RotateRight, g, r - 1], n]
matmul[a_, b_, r_, n_] := Mod[
{{polmul[a[[1, 1]], b[[1, 1]], r, n] + polmul[a[[1, 2]], b[[2, 1]], r, n],
polmul[a[[1, 1]], b[[1, 2]], r, n] + polmul[a[[1, 2]], b[[2, 2]], r, n]},
{polmul[a[[2, 1]], b[[1, 1]], r, n] + polmul[a[[2, 2]], b[[2, 1]], r, n],
polmul[a[[2, 1]], b[[1, 2]], r, n] + polmul[a[[2, 2]], b[[2, 2]], r, n]}}, n]
matsq[a_, r_, n_] := matmul[a, a, r, n]
matpow[a_, k_, r_, n_] := If[k == 1, a,
If[EvenQ[k],
matpow[matsq[a, r, n], k/2, r, n],
matmul[a, matpow[matsq[a, r, n], (k - 1)/2, r, n], r, n]
]
]
xmat[r_, n_] :=
{{PadRight[{0, 2}, r], PadRight[{n - 1}, r]},
{PadRight[{1}, r], ConstantArray[0, r]}}
isprime[n_] := With[{r = smallestr[n]},
If[r == 0, n == 2,
With[{xp = matpow[xmat[r, n], n - 1, r, n]},
Mod[RotateRight[xp[[1, 1]]] + xp[[1, 2]], n]
=== PadRight[Append[ConstantArray[0, Mod[n, r]], 1], r]
]
]
]
where smallestr is as in my other answer.
Running this on $n$ up to 100000 (all answers correct) gives the following timing:
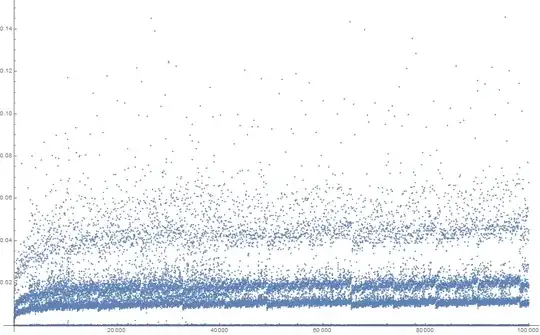
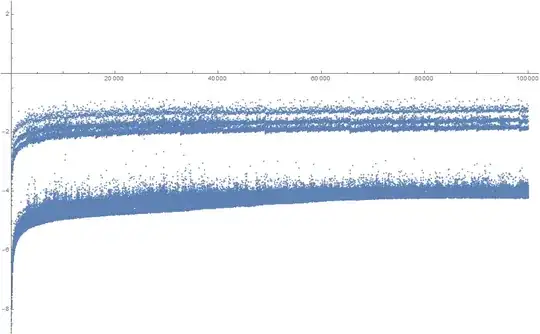
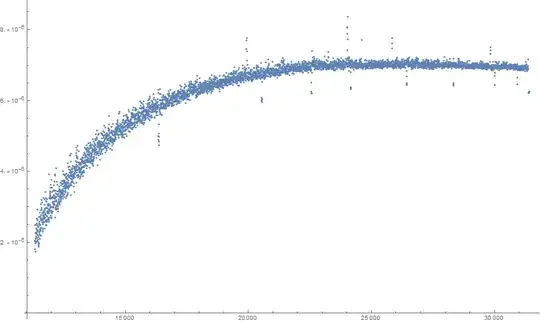
Seems that it is of at worst logarithmic order (as that answer by Lucia suggests) - actually the graph of $\log(\operatorname{time}(n))/\log\log(n)$ looks almost like going to be bounded above:
Since the algorithm involves a recursive procedure for matrix powers, in principle one also has to check memory use. Here I must confess results are strange, maybe it is something hardware-specific.
$$
\begin{array}{r|l}
\text{amount of memory}&\text{number of cases (out of 100000)}\\
\hline
32&1407\\
64&94408\\
80&1\\
288&1\\
320&42\\
352&3\\
392&8\\
424&2316\\
456&1812\\
3452552&1
\end{array}
$$
This last amount 3452552 corresponds to $n=65969$, I have no idea why it needed so much memory. As I said this might be something machine specific - maybe some garbage collection occurred at that point or something like that. Anyway, as opposed to memory measurement timing data seem to be very accurate, I used the Mathematica command AbsoluteTiming and documentation says it gives actual processor time used for the calculation with quite high precision.


PARI/GP interpreter crashed -- automatically restarting. *** at top-level: if(Mod((polchebyshev(n,1,x))%(x^r-1),n)-( *** ^-------------------- *** incorrect type in gtos [integer expected] (t_POL).– მამუკა ჯიბლაძე Nov 17 '17 at 14:57