There is a number $n \in \mathbb{N}, \ n > 1, n < 2^k$. How to prove this statement:
$n$ is included into Pascal triangle not more than $2k -2$ times?
Asked
Active
Viewed 297 times
2
Alexey Ustinov
- 11,875
Vremennik
- 31
-
2Where does this question come from? – Igor Rivin Dec 30 '17 at 17:55
-
3From the way you phrase your question, you seem to know that this is a true statement. Where does that knowledge come from? – André Henriques Dec 30 '17 at 17:58
-
3In addition to the problems with lack of context, this question is cross-posted to MSE. – Steven Landsburg Dec 30 '17 at 18:09
-
similar question: https://mathoverflow.net/questions/28717/singmasters-conjecture – Pietro Majer Dec 30 '17 at 18:14
-
The m.se post is https://math.stackexchange.com/questions/2585658/a-question-about-pascal-triangle – Gerry Myerson Dec 30 '17 at 19:15
-
1Since the question appears to be an open research problem, I am not sure why this was closed. Voting to reopen. – Igor Rivin Dec 30 '17 at 19:44
-
@Igor Rivin As said above, this question has been posted simultaneously on Math.stackexchange without mentionning the double posting... – Jean Marie Becker Jan 01 '18 at 01:37
1 Answers
4
This is a result of Singmaster (American Math Monthly, 1971).
Here is his proof ($N(a)$ is the number of times $a$ appears.) This result has since been much improved, see the wikipedia article on Singmaster's conjecture.
To elaborate somewhat, Abbott-Erdos-Hanson show:
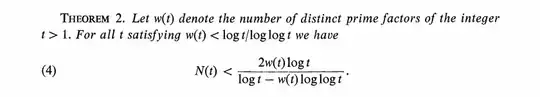and use this to show the better asymptotic bound. It is not quite clear how to use this to get better bounds for all $t.$
Igor Rivin
- 95,560
-
The proof gives $N(a)\le2+2\log_2a$, and OP wants $N(a)\le2k-2$ when $a<2^k$, which is a little bit stronger (but maybe the improved results in the wikipedia essay give what's needed). – Gerry Myerson Dec 30 '17 at 19:14
-
@GerryMyerson The results in the wikipedia link are asymptotically better, so they definitely do the trick. I did not notice the plus vs minus, mea culpa. – Igor Rivin Dec 30 '17 at 19:21
-
if they're asymptotically better, then they do the trick for $a$ sufficiently large, but not necessarily for all $a$, right? – Gerry Myerson Dec 30 '17 at 19:24
-
2@GerryMyerson See the edit. It is not clear that one can get the better result for ALL $t$ using this technology. – Igor Rivin Dec 30 '17 at 19:38