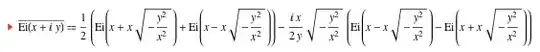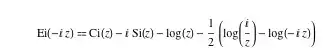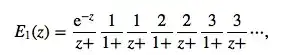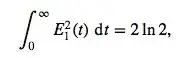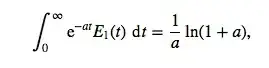4

I noticed that the following function

$$\mbox{Ei}(x) := - \int_{-x}^{\infty}\frac{e^{-t}}{t} \,\mathrm d t$$

occurs increasingly in different areas of physics and in mathematics.

I am wondering if anyone knows of any interesting functional or algebraic properties it possesses that might make its applications more efficient. After scouring different sources I have not found any, but have seen it trivially related to other functions such as the incomplete gamma function or the sine and cosine integrals.

Rodrigo de Azevedo
  • 1
John Joe
  • 141
  • I did not find exactly what you ask for. But I will provide two general answers anyway. – Gerald Edgar Apr 10 '18 at 11:51
  • Thank you for bringing these up. While these are interesting, I am hoping for something more along the lines of useful functional properties like f(x+1)=xf(x) or f(x+y)=f(x)f(y), information that can more precisely point-point the nature of the function and how it can be used without directly relying on an analytic representation. – John Joe Apr 10 '18 at 15:38

2 Answers2

5

One place to look on questions like this is the Wolfram Functions site.

The entry ExpIntegralEi has 183 formulas.

Here are two examples:

image1

image2

Community
  • 1
Gerald Edgar
  • 40,238
  • The formulas for sin(x+y) and the like are in the Transformations section of the page for sin, but there’s nothing really like that on the page for Ei. –  Apr 10 '18 at 16:51
5

Another place to look on questions like this is the NIST Digital Library of Mathematical Functions

Here is Chapter 6 Exponential, Logarithmic, Sine, and Cosine Integrals

Some examples, in terms of the related exponential integral $E_1(z) = \int_z^\infty \frac{e^{-t}}{t}\;dt$

continued fraction

continued fraction

integrals

enter image description here enter image description here

At the end they discuss methods of computation, approximations, and software.

Gerald Edgar
  • 40,238