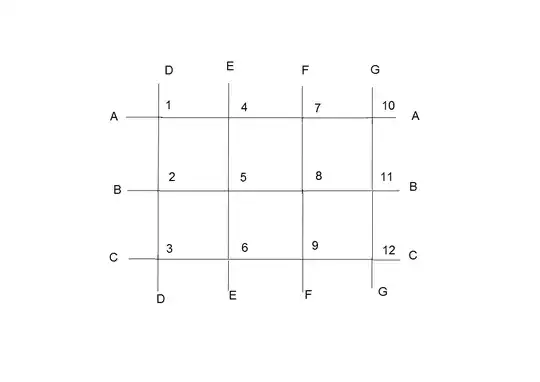
What is the coefficient $c$ of the term $x_1^2x_2^2x_3^2\cdots x_{12}^2$ in the expansion of the following multivariable polynomial:
$(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_{10})(x_2-x_3)(x_2-x_5)(x_2-x_{11})(x_3-x_6)(x_3-x_{12})(x_4-x_5)(x_4-x_6)(x_4-x_7)(x_5-x_6)(x_5-x_8)(x_6-x_9)(x_7-x_8)(x_7-x_9)(x_7-x_{10})(x_8-x_9)(x_8-x_{11})(x_9-x_{12})(x_{10}-x_{11})(x_{10}-x_{12})(x_{11}-x_{12})$
If we recognized each $x_i$ as a vertex and each factor as a edge, then we get a quadrilateral tessellation of the torus. The above polynomial is actually as the graph polynomial of the following quadrangulation of the torus:
I hope someone can give an algorithm to get the coefficient of the term $x_1^2x_2^2x_3^2\cdots x_{12}^2$ in the expansion of the above graph polynomial. Thank you very much!