Cops & Robbers is a certain pursuit-evasion game between two players, Alice and Bob. Alice is in charge of the Justice Bureau, which controls one or more law enforcement officers, the cops. Bob controls a single robber, a guy whose main concern is to evade the cops at any costs. Both deploy their guys on the vertices of a city, a simple graph, and start a manhunt under the following natural rules:
On her turn, Alice chooses a (possibly empty) subset of the cops and moves them to some adjacent vertices.
On his turn, Bob may either move his robber to an adjacent vertex or stay still.
The game ends with a win for Alice whenever any of her cops manages to occupy the same vertex as the robber. Bob wins if this never happens in the game.
Cops & Robbers and its variants have been studied on finite graphs so extensively, while little is known in the case of the infinite graphs, particularly those of uncountable cardinality which are the subject of this question. One may take a look at the following references for a fairly comprehensive account of the topic (including some results concerning the infinite version) or watch this and this episodes of PBS Infinite Series show by Kelsey Houston-Edwards:
Bonato and Nowakowski, The Game of Cops and Robbers on Graphs, 2011.
Florian Lehner, Cops, robbers, and infinite graphs, 2014.
Jordan DuBeau and Beth Matys, Cops and Robbers on Infinite Graphs, 2015.
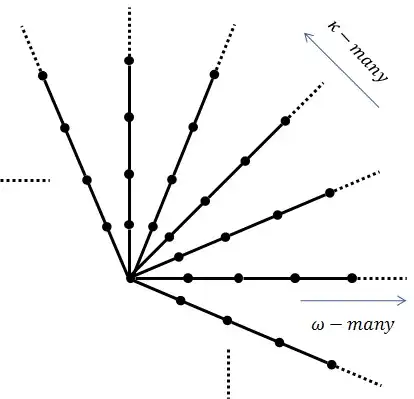
The cop number of a graph is the minimum number of the cops that Alice needs to have a winning strategy in the game. A graph with cop number $1$ is called cop-win. Otherwise, it is called robber-win. Before getting into the main question, let's observe that the cop number of a large infinite graph may or may not be large. For instance, $K_{\kappa}$ and $S_{\kappa}$, the complete and star graph of size $\kappa$, are clearly cop-win and therefore have the cop number $1$. In contrary, the totally disconnected graph of size $\kappa$ has the cop number $\kappa$. Some other examples are the infinite path $P_{\infty}$, and Rado graph, $\mathcal{R}$, which have the cop number $\aleph_0$.
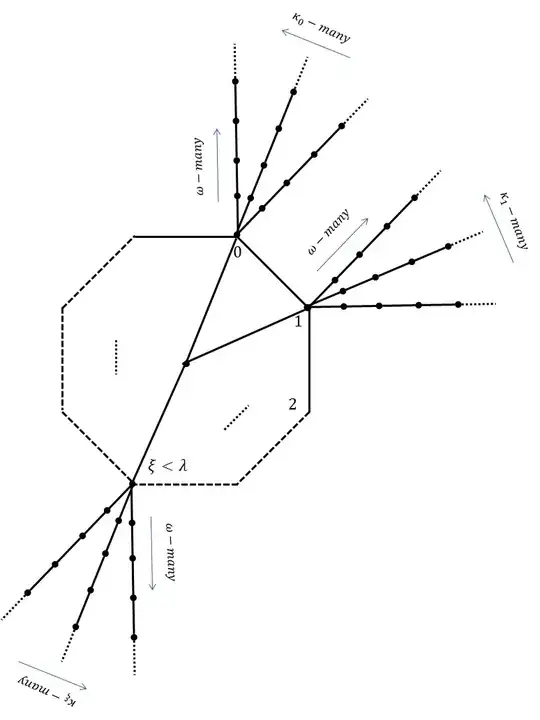
Definition. We call connected infinite graphs with minimum and maximum possible cop-numbers (i.e. $1$ and $|G|$), law and crime neighborhoods respectively. A Mega City is an infinite connected graph, $M$, with the "dystopian" property that $M$ contains either a law or a crime neighborhood as big as $|M|$ as its sub-graph. An uncountable cardinal $\kappa$ is a Dredd cardinal (named after Judge Dredd) if every connected graph of size $\kappa$ is a Mega City.
The first question is about the possible large cardinal strength of the existence of such a Ramsey-like cardinal.
Question 1. Is there any Dredd cardinal? What is their large cardinal strength in comparison with other large cardinals of some Ramsey characterization such as weakly compact, Erdős, and Ramsey cardinals?
Remark 1. An approach towards question 1 might be through considering $\kappa$-Aronszajn trees and checking the tree property which provides a characterization of weakly compact cardinals. Maybe one can relate the cofinal branches in a $\kappa$-tree to the law or crime neighborhoods in a Mega City of size $\kappa$, given the fact that trees and paths are rather simple cities to analyze for the game of cops and robbers. Also, as Will mentioned in his comments here and here, in the definition of a Mega-City the connectedness assumption is essential for the whole graph and crime neighborhoods in order to avoid easy constructions.
The next question is about the possible characterization of infinite connected graphs with arbitrary cop-numbers.
Question 2. Let $\kappa$ be an infinite cardinal and $1\leq \lambda\leq \kappa$. Is there a connected graph of size $\kappa$ and cop number $\lambda$? How many graphs of this type are there up to isomorphism (for any given $\kappa$, $\lambda$)?
Remark 2. Concerning the question 2 in the special cases such as $\kappa=2^{\aleph_0}$, an approach could be thinking about using cardinal characteristics of the continuum for constructing examples of connected (directed) graphs of size continuum with cop numbers strictly less than $2^{\aleph_0}$. In order to observe this, note that cop number of any graph is less than or equal to its domination number because one may catch the robber in the first move simply by deploying one cop on each vertex in a minimal dominating set of the graph. The idea is that the set-theoretic dominating number, $\mathfrak{d}$, serves as the domination number of a graph, $G$, of size $2^{\aleph_{0}}$ (don't confuse the similar terms in set theory and graph theory with each other). At the request of Monroe, let me clarify the example a little bit more:
$G$ is defined by the sequence domination relation between reals (i.e. functions $f:\omega\rightarrow \omega$). In this graph, the vertex labeled by $g$ is adjacent to $f$ (i.e. $g\rightarrow f$) if $g$ dominates $f$ as a sequence (denoted by $f\leq^* g$) that is $f(n)\leq g(n)$ for all but finitely many $n\in \omega$. Now a dominating family, $\mathcal{F}$, of sequences for the entire real numbers is a set of functions from $\omega $ to $\omega$ such that every such function is either in $\mathcal{F}$ or is $\leq^*$-dominated by a member of $\mathcal{F}$ (i.e. $\mathcal{F}$ is a domination set of $G$ in the graph-theoretic sense) and $\mathfrak{d}$ is defined to be the minimum size of such a family (i.e. the domination number of the graph $G$). Consequently we have $c(G)\leq \mathfrak{d}\leq 2^{\aleph_0}$ (which $c(G)$ stands for the cop number of $G$). Finally using forcing one may make $\mathfrak{d}<2^{\aleph_0}$ and so the cop number of the graph $G$ in the generic extension will be strictly smaller than $2^{\aleph_{0}}$.
However, one should note that generally, the domination number is a very loose upper bound for the cop number of a graph. (Certainly, the Justice Bureau has much more clever strategies to control the crime rate in the city rather than placing a cop right in the front of every single home!) For instance, the domination number of the dodecahedron graph (of size $20$) is $7$ while its cop-number is only $3$. Here, the following question arises:
Question 3. What is the cop-number of $G$, the sequence domination graph of size continuum described in the previous remark? Can it be countable? If not, what is the precise value of this new cardinal characteristic of continuum and how does it relate to the other entities in the Cichoń's diagram?