This isn't an answer to conjecture 1, just an elaboration of things others mentioned.
There is every reason to think that the answer to conjecture 1 is yes and even that for fixed $m \gt 1$ we have that for each odd integer $x \geq 3$ there are infinitely many $n$ with $p_{n+m}-p_n-p_m=x.$ We don't know that there is even one, however we can say with good precision how the number of solutions should be expected to grow as $n \rightarrow \infty.$ Computations always (seem) to conform to this with good fidelity as far as checked. I'll explain that a bit and then point out that that fixing $m=2$ would likely not be the most fruitful way to find a solution.
So with $m=3$ and $p_3=5$ solving $p_{n+3}-p_n-5=15$ amounts to finding two primes $p_N$ and $p_n$ with
We do not know that $p_N-p_m=20$ infinitely often. For each even integer g define $\pi_g(X)$ to be the number of pairs $(p_N,p_n)$ with $p_N-p_n=g$ and $p_N \leq X.$ Then $\pi_2(X)$ is the number of twin primes up to $X$ We don't know that this grows without bound but can expect that it is assymptotic (in some sense which could be made precise) to $C_2\frac{X}{\ln^2X}$ and that the constant $C_2=\prod_p(1-\frac1{(p-1)^2})$ with the product over the odd primes.
There is a similar constant $C_g$ for each even $g.$ Namely $C_g=C_2\prod_p\frac{p-1}{p-2}$ where the product is over odd primes which divide $g.$
So $p_n+20$ is expected to be prime more often that $p_2$ but about as often as $p+10.$ i.e. $\pi_{20}(X) \sim \pi_{10}(X)\sim \frac{4}{3}\pi_2(X).$ That is a prediction which holds up quite well as far as checked.
For an amazing exposition of this read Heuristic Reasoning In The Theory of Numbers by Polya.
But our goal had an extra condition. Want something like to have
$p_n,p_n+6,p_n+14,p_n+20$ to all be prime but $p_n+h$ be composite for $h=2,4,8,10,12,16,18.$ It is possible to similarly predict how often that happens up to $X.$ Summing over finite number of cases would give a prediction for the number of solutions of the given problem.
$m=2$ is a little easier but I wanted to use a different value.
But where is it most fruitful to look for solutions to $p_{n+m}-p_n-p_m=x$?
Here is a graph for $p_{n+m}-p_n-p_m=101$ with $n+m\lt 200.$
I find $168$ solutions. here is a graph.
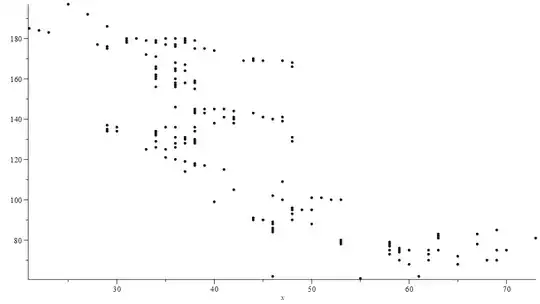
Of the $168$ solutions, $61$ of them have $m \in\{34,35,36,37,38\}$ and the ratio $\frac{n}{m}$ ranges from $3$ to $5.2$
Using $p_k \sim {k}{\ln{k}}$ one might be able to argue that for fixed $r=\frac{n}{m}$ ( really $r$ in some small range like $[3,5]$) there is a narrow range of $m$ values that would be worth searching first. Perhaps the best $r$ (given $x$) could be estimated. I would have guessed $r \sim 1$ is best, but that seems not to be the case based on this one computation. Perhaps the optimal range is past $m+n=200.$

@symbol. – Pierre-Yves Gaillard Jul 03 '18 at 16:57