3

I am working in a computing environment that has the facility to compute general nD convex hulls and not much else in the way of computational geometry. The routine, given a set of points, gives the vertices of the convex hull and edge connectivity information.

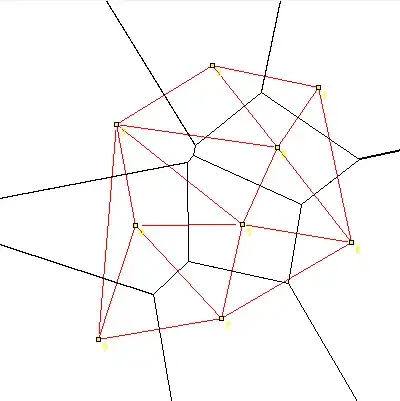
I want to use this method to compute the (bounded) Voronoi diagram of a set of 2D points. Some literature research (e.g. this paper) shows that you can "lift" the 2D points by adding a third coordinate, and then generate the convex hull of those points. The faces of the convex hull can then be projected to get the Delaunay triangulation, while computing the normals of those faces yields the Voronoi vertices.

My problem is that although I am able to use this approach to compute the inner Voronoi vertices in a bounded diagram, I am unable to use this to compute the frontier vertices (the intersection of the infinite rays in the diagram with the rectangular bounds). I may not have searched enough, but I was unable to find information on how to do so.

One possibility I thought of was to find the intersecting half-spaces on each vertex of the 2D convex hull (including the rectangle bounds), but I was wondering if there are more efficient/elegant approaches. Literature pointers will be immensely appreciated.

richard aspeto
  • 31

1 Answers1

1

Each edge of the convex hull of the Delaunay triangulation is the edge of a unique triangle. Each of these triangles determines an infinite ray of the Voronoi diagram. So once you have identified these rays, you can then intersect each with a bounding box. Now your problem reduces to ray-box intersection.

If you search for "ray-box intersection," you'll find a variety of algorithms, from the straightforward to those that minimize calculations. This also goes under the name line clipping.

          VorD
          (Image from ImageJ.)
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 2
    Wow, I actually just asked for Computational Geometry in C by interlibrary loan, and was not inspecting an answer from the author himself! Thank you very much! So, if I understand you right: I should just construct the infinite rays of the unbounded Voronoi diagram from the circumcenters and "outermost" bisectors of the outermost Delaunay triangles, and just intersect them with the bounding box? – richard aspeto Sep 20 '18 at 12:51
  • (Also, another reason why I asked my question is that I eventually want to make power/Laguerre diagrams as well, and I understand that there is a completely analogous procedure to the Voronoi case.) – richard aspeto Sep 20 '18 at 12:54