What's your favorite equation, formula, identity or inequality?

Question

Certain formulas I really enjoy looking at like the Euler-Maclaurin formula or the Leibniz integral rule. What's your favorite equation, formula, identity or inequality?

Answer 1

Stokes' Theorem $$\int_M\mathrm{d}\omega=\oint_{\partial M}\omega.$$

Answer 2

Trivial as this is, it has amazed me for decades:

$(1+2+3+\cdots+n)^2=1^3+2^3+3^3+\cdots+n^3.$

Answer 3

There are many, but here is one.

$d^2=0$

Answer 4

$$ \frac{24}{7\sqrt{7}} \int_{\pi/3}^{\pi/2} \log \left| \frac{\tan t+\sqrt{7}}{\tan t-\sqrt{7}}\right| dt\\ = \sum_{n\geq 1} \left(\frac n7\right)\frac{1}{n^2}, $$ where $\left(\frac n7\right)$ denotes the Legendre symbol. Not really my favorite identity, but it has the interesting feature that it is a conjecture! [Update: the conjecture was proved in 2010, https://arxiv.org/abs/1005.0414.] It is a rare example of a conjectured explicit identity between real numbers that can be checked to arbitrary accuracy. This identity has been verified to over 20,000 decimal places. See J. M. Borwein and D. H. Bailey, Mathematics by Experiment: Plausible Reasoning in the 21st Century, A K Peters, Natick, MA, 2004 (pages 90-91).

Answer 5

There's lots to choose from. Riemann-Roch and various other formulas from cohomology are pretty neat. But I think I'll go with

$$\sum\limits_{n=1}^{\infty} n^{-s} = \prod\limits_{p \text{ prime}} \left( 1 - p^{-s}\right)^{-1}$$

Answer 6

Mine is definitely $$1+\frac{1}{4}+\frac{1}{9}+\cdots+\frac{1}{n^2}+\cdots=\frac{\pi^2}{6},$$ an amazing relation between integers and pi.

Answer 7

$e^{\pi i} + 1 = 0$

Answer 8

$$1+2+3+4+5+\cdots = -\frac1{12}\,,$$ once suitably regularised of course :-)

Answer 9

$$\frac{1}{1-z} = (1+z)(1+z^2)(1+z^4)(1+z^8)...$$

Both sides as formal power series work out to $1 + z + z^2 + z^3 + ...$, where all the coefficients are 1. This is an analytic version of the fact that every positive integer can be written in exactly one way as a sum of distinct powers of two, i. e. that binary expansions are unique.

Answer 10

I'm currently obsessed with the identity $\det (\mathbf{I} - \mathbf{A}t)^{-1} = \exp \text{tr } \log (\mathbf{I} - \mathbf{A}t)^{-1}$. It's straightforward to prove algebraically, but its combinatorial meaning is very interesting.

Answer 11

$V - E + F = 2$

Euler's characteristic for connected planar graphs.

Answer 12

$196884 = 196883 + 1$

Answer 13

For a triangle with angles a, b, c $$\tan a + \tan b + \tan c = (\tan a) (\tan b) (\tan c)$$

Answer 14

Given a square matrix $M \in SO_n$ decomposed as illustrated with square blocks $A,D$ and rectangular blocks $B,C,$

$$M = \left( \begin{array}{cc} A & B \\\ C & D \end{array} \right) ,$$

then $\det A = \det D.$

What this says is that, in Riemannian geometry with an orientable manifold, the Hodge star operator is an isometry, a fact that has relevance for Poincare duality.

https://en.wikipedia.org/wiki/Hodge_duality

https://en.wikipedia.org/wiki/Poincar%C3%A9_duality

But the proof is a single line:

$$ \left( \begin{array}{cc} A & B \\\ 0 & I \end{array} \right) \left( \begin{array}{cc} A^t & C^t \\\ B^t & D^t \end{array} \right) = \left( \begin{array}{cc} I & 0 \\\ B^t & D^t \end{array} \right). $$

Answer 15

I always thought this one was really funny: $1 = 0!$

Answer 16

It's too hard to pick just one formula, so here's another: the Cauchy-Schwarz inequality:

||x|| ||y|| >= |(x.y)|, with equality iff x&y are parallel.

Simple, yet incredibly useful. It has many nice generalizations (like Holder's inequality), but here's a cute generalization to three vectors in a real inner product space:

||x||² ||y||² ||z||² + 2(x.y)(y.z)(z.x) >= ||x||²(y.z)² + ||y||²(z.x)² + ||z||²(x.y)², with equality iff one of x,y,z is in the span of the others.

There are corresponding inequalities for 4 vectors, 5 vectors, etc., but they get unwieldy after this one. All of the inequalities, including Cauchy-Schwarz, are actually just generalizations of the 1-dimensional inequality:

||x|| >= 0, with equality iff x = 0,

or rather, instantiations of it in the 2^nd, 3^rd, etc. exterior powers of the vector space.

Answer 17

I think that Weyl's character formula is pretty awesome! It's a generating function for the dimensions of the weight spaces in a finite dimensional irreducible highest weight module of a semisimple Lie algebra.

$$\operatorname{ch}(V)=\frac{\sum_{w\in W}(-1)^{\ell(w)}w\left(e^{\lambda+\rho}\right)}{e^\rho\prod_{\alpha>0}\left(1-e^{-\alpha}\right)}$$

Answer 18

Gauss-Bonnet, even though I am not a geometer.

Answer 19

The formula $\displaystyle \int_{-\infty}^{\infty} \frac{\cos(x)}{x^2+1} dx = \frac{\pi}{e}$. It is astounding in that we can retrieve $e$ from a formula involving the cosine. It is not surprising if we know the formula $\cos(x)=\frac{e^{ix}+e^{-ix}}{2}$, yet this integral is of a purely real-valued function. It shows how complex analysis actually underlies even the real numbers.

Answer 20

It may be trivial, but I've always found

$\sqrt{\pi}=\int_{-\infty}^{\infty}e^{-x^{2}}dx$

to be particularly beautiful.

Answer 21

It has to be the ergodic theorem, $$\frac{1}{n}\sum_{k=0}^{n-1}f(T^kx) \to \int f\:d\mu,\;\;\mu\text{-a.e.}\;x,$$ the central principle which holds together pretty much my entire research existence.

Answer 22

$2^n>n $

Answer 23

Euclid, Elements, Book1 Prop 47:

Ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν τετραγώνοις.

That is,

In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.

Answer 24

Riemann-Roch, and its generalizations:

Hirzebruch-Riemann-Roch

Grothendieck-Hirzebruch-Riemann-Roch

Atiyah-Singer (which is also a generalization of Gauss-Bonnet)

Is it cheating to put all of these in a single answer? :-)

Answer 25

$\left(\frac{p}{q}\right) \left(\frac{q}{p}\right) = (-1)^{\frac{p-1}{2} \frac{q-1}{2}}$.

Answer 26

My favorite is the Koike-Norton-Zagier product identity for the j-function (which classifies complex elliptic curves):

j(p) - j(q) = p^-1 \prod_m>0,n>-1 (1-p^mqⁿ)^c(mn),

where j(q)-744 = \sum_{n >-2} c(n) qⁿ = q^-1 + 196884q + 21493760q² + ... The left side is a difference of power series pure in p and q, so all of the mixed terms on the right cancel out. This yields infinitely many identities relating the coefficients of j.

It is also the Weyl denominator formula for the monster Lie algebra.

Answer 27

$${\mathbb E}[X+Y]={\mathbb E}[X]+{\mathbb E}[Y]$$ for any two random varibles $X$ and $Y$.

Answer 28

$ D_A\star F = 0 $

Yang-Mills

Answer 29

For X a based smooth manifold, the category of finite covers over X is equivalent to the category of actions of the fundamental group of X on based finite sets:

                       \pi-sets   ===     et/X

The same statement for number fields essentially describes the Galois theory. Now the idea that those should be somehow unified was one of the reasons in the development of abstract schemes, a very fruitful topic that is studied in the amazing area of mathematics called the abstract algebraic geometry. Also, note that "actions on sets" is very close to "representations on vector spaces" and this moves us in the direction of representation theory.

Now you see, this simple line actually somehow relates number theory and representation theory. How exactly? Well, if I knew, I would write about that, but I'm just starting to learn about those things.

(Of course, one of the specific relations hinted here should be the Langlands conjectures, since we're so close to having L-functions and representations here!)

Answer 30

$\prod_{n=1}^{\infty} (1-x^n) = \sum_{k=-\infty}^{\infty} (-1)^k x^{k(3k-1)/2}$

Answer 31

The Euler-Lagrange equations, $$\frac{\partial L}{\partial q_j} = \frac{d}{dt}\frac{\partial L}{\partial \dot{q}_j}$$

Answer 32

The Pythagorean Theorem for Right-Corner Tetrahedra[*]:

Euclidean: $A^2 + B^2 + C^2 = D^2$

Hyperbolic: $\cos\frac{A}{2} \cos\frac{B}{2} \cos\frac{C}{2} \; - \; \sin\frac{A}{2} \sin\frac{B}{2} \sin\frac{C}{2} = \cos\frac{D}{2}$

Spherical: $\cos\frac{A}{2} \cos\frac{B}{2} \cos\frac{C}{2} \; + \; \sin\frac{A}{2} \sin\frac{B}{2} \sin\frac{C}{2} = \cos\frac{D}{2}$

where $A$, $B$, $C$ are the areas of the "leg-faces" and $D$ is the area of the "hypotenuse-face".

For right-corner simplices in higher Euclidean dimensions, we have that the sum of the squares of the content of leg-simplices equals the square of the content of the hypotenuse-simplex. (I don't happen to know the non-Euclidean counterparts of this generalization. Perhaps this makes for a good MO question!)

As generalizations of the Pythagorean Theorem for Triangles, I always found these (Euclidean) results to be more satisfying than the diagonal-of-a-box/distance formulas: instead of dealing only with segments, we have that, as the dimension of the ambient space goes up, so does the dimension of the objects involved in the relations.

[*] Edges meeting at the "right corner" are mutually orthogonal.

Answer 33

Addendum to $e^{i \pi}$

Benjamin Peirce apparently liked this mathematical synonym for the additive inverse of $1$ so much that he introduced three special symbols for $e, i, \pi$ — ones that enable $e^{i \pi}$ to be written in a single cursive ligature, like so:

• Benjamin Peirce (1870/1882), Linear Associative Algebra, § 15, p. 5.

Answer 34

$\pi = 2 \times 1/\sqrt(1/2) \times 1/\sqrt((1+\sqrt(1/2))/2) \times 1/\sqrt((1+\sqrt((1+\sqrt(1/2))/2))/2) \times \ldots $

Answer 35

Cauchy integral formula $$ f(z)=\frac{1}{2\pi i}\int_{\gamma}\frac{f(w)}{w-z} dw $$

Answer 36

My favorite equation is

$$\frac{16}{64} = \frac{1}{4}.$$

What makes this equation interesting is that canceling the $6$'s yields the correct answer. I realized this in, perhaps, third grade. This was the great rebellion of my youth. Sometime later I generalized this to finding solutions to

$$\frac{pa +b}{pb + c} = \frac{a}{c}.$$

where $p$ is an integer greater than $1$. We require that $a$, $b$, and $c$ are integers between $1$ and $p - 1$, inclusive. Say a solution is trivial if $a = b = c$. Then $p$ is prime if and only if all solutions are trivial. On can also prove that if $p$ is an even integer greater than $2$ then $p - 1$ is prime if and only if every nontrivial solution $(a,b,c)$ has $b = p - 1$.

The key to these results is that if $(a, b, c)$ is a nontrivial solution then the greatest common divisor of $c$ and $p$ is greater than $1$ and the greatest common divisor of $b$ and $p - 1$ is also greater than $1$.

Two other interesting facts are (i) if $(a, b, c)$ is a nontrivial solution then $2a \leq c < b$ and (2) the number of nontrivial solutions is odd if and only if $p$ is the square of an even integer. To prove the latter item it is useful to note that if $(a, b, c)$ is a nontrivial solution then so is $(b - c, b, b - a)$.

For what it is worth I call this demented division.

Answer 37

$(A-\lambda _1) (A-\lambda _2) \ldots = 0$, the Cayley-Hamilton theorem.

Answer 38

Bayes equations: $${\mathbb P}(A|B) = {\mathbb P}(A∩B)/{\mathbb P}(B).$$ It is the basis of conditional probability.

Answer 39

The Spectral theorem for normal operators on a Hilbert space:

$T = \int_{\sigma (T)} \lambda dP(\lambda)$

where $\sigma (T)$ is the spectrum of $T$ and $P$ is a regular projection-valued measure supported on $\sigma (T)$.

Answer 40

$\sin^2 A + \cos^2 A = 1$

Answer 41

$$Var[X+Y]=Var[X]+Var[Y]$$ for any two independent random variables $X$ and $Y$, which is the statistics equivalent of the Pythagorean Theorem.

Answer 42

Pick's theorem $A = I + \frac 1 2 B - 1$, where $A$, $I$, and $B$ are the area, number of interior integer points, and number of boundary integer points, respectively, of a polygon with vertices on the integer lattice. Picks identity is fascinating because it computes a continuous quantity completely discretely. (Of course, this is not quite correct, since we have quite a discrete requirement about the vertices of the polygon.) Also, the "1" is not an accident, but the Euler characteristic of the polygon (and so there are various natural extensions of Pick's theorem).

Answer 43

One that I just learned recently is $$ (1 + q + q^3 + q^6 + q^{10} + q^{15} + \cdots)^4 = \sum_{k=0}^\infty \sigma(2k+1)q^k $$ which states that the number of ways of writing an integer $k$ as a sum of exactly 4 triangular numbers (paying attention to ordering) is equal to the sum of divisors of $2k+1$.

If that isn't cool and surprising, I don't know what is.

Answer 44

The Newton iteration for finding the inverse, X, of a matrix A:

X_i+1 = 2 * X_i - X_i * A * X_i

Completely impractical and yet so beautiful. The first time I saw a Newton iteration working I thought it was "magical".

Answer 45

Well, of course my favorite is Stokes theorem (it used to be the background of my mobile in the old days where you still manually designed monochromatic backgrounds pixel by pixel), but that is already suggested. And so are many others. So I'll go for Kontsevich formula for the number $N_d$ of rational curves through $3d-1$ generic points in the plane:

$N_d + \sum_{\stackrel{d_A, d_B \geq 1}{d_A + d_B = d}} \binom{3d - 4}{3 d_A - 1} N_{d_A} N_{d_B} d_A^3 d_B = \sum_{\stackrel{d_A, d_B \geq 1}{d_A + d_B = d}} \binom{3d - 4}{3 d_A - 2} N_{d_A} N_{d_B} d_A^2 d_B^2$

Although I admit this looks ugly until you see the proof. Then it becomes so neat!

Answer 46

I think this fits the original question's request for something nice-looking: $\binom{2n}{n}=(-4)^n\binom{-1/2}{n}$

Answer 47

I have a soft spot for Heine's formula from the theory of orthogonal polynomials (since the proof is such a pretty calculation):

If $\mu$ is a measure with finite moments $\beta_k=\int x^k d\mu(x)$, then

$$\det(\beta_{i+j})_{i,j=0,\ldots,k-1} = \frac{1}{k!} \int \cdots \int \Delta(x_1,\ldots,x_k)^2 d\mu(x_1) \cdots d\mu(x_k)$$

where $\Delta$ is the Vandermonde determinant.

Answer 48

I'm a fan of $\Omega SU \simeq BU$.

Answer 49

The isogeny theorem: $$\mathrm{Hom}_K(A,A') = \mathrm{Hom}_{G_K}(T_\ell(A),T_\ell(A')).$$

Answer 50

Lately, I really like the Greenlees-May duality: $RHom_A(R\Gamma_{\mathfrak{a}}M,N) \cong RHom_A(M,L\Lambda_{\mathfrak{a}}N)$ which holds for any pair of complexes over a noetherian ring.

Answer 51

Ky Fan's inequality seems rather beautiful. The most beautiful proof can be found here

Jovanović, Milan V.; Pogány, Tibor K.; Sándor, József, Notes on certain inequalities by Hölder, Lewent and Ky Fan, J. Math. Inequal. 1, No. 1, 53-55 (2007). ZBL1147.26011, MR2347705.

Answer 52

The Gauss Formula from Riemannian geometry:

$\overline{\nabla}_XY = \nabla_XY + \text{II}(X,Y)$

It may just be a decomposition into tangential and normal parts, but I find it very aesthetically pleasing. (It's also not completely immediate that the tangential part of the ambient connection should actually be the intrinsic connection.)

Answer 53

How about $\displaystyle \sigma_7(n)=\sigma_3(n)+120\sum_{k=1}^{n-1} \sigma_3(k) \sigma_3(n-k)$? This is an utterly shocking result, and the only known proof uses complex analysis.

Answer 54

The braid relation is probably my favorite equation, algebraically capturing the Reidemeister III move as $x y x = y x y$. Although to a younger person, I still find that suggesting that 5 is not prime is reliably charming revelation: $5 = (2 + i)(2 - i)$.

Answer 55

There are many beautiful equations above, so I'll be a bit different and add something nonsensical. Namely

$$\langle f\rangle = \frac{\int_\ast f(\phi)e^{\frac{\mathrm{i}}{\hbar}\int_M\mathcal{L}(\phi)}\mathcal{D}\phi}{\int_\ast e^{\frac{\mathrm{i}}{\hbar}\int_M\mathcal{L}(\phi)}\mathcal{D}\phi}.$$

Just insert your favourite spacetime manifold $M$ and the classical Lagrangian $\mathcal{L}$ of your choice, and you get to learn the expectation value of any physical observable $f$... as soon as you figure out what the hell $\ast$ and $\mathcal{D}\phi$ are, that is.

Answer 56

$\sum_{i=1}^m \sum_{j=1}^n a_{ij} = \sum_{j=1}^n \sum_{i=1}^m a_{ij}$

Answer 57

$$e=\lim_{n\to\infty}\sqrt[p_n]{\prod_{k=1}^np_n}$$ as seen at Gaussianos

$(\prod_{k=1}^np_n=p_n$# which is the primorial of the nth prime number $p_n)$

Answer 58

I'm surprised that nobody said

$e=mc^2$

Answer 59

I learned Quantum Mechanics and Linear Algebra in tandem, so Schrodinger's linear time-independent equation has always had a special place in my heart. It shows that eigenvalues and eigenvectors are fundamental to our description of atomic physics. Also treating observables as operators was a great conceptual revolution.

$H\psi=E\psi$

Answer 60

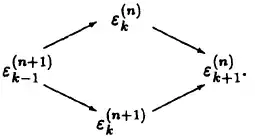
With the stuff I've seen in the literature of sequence transformations, I've started to love the formulae for Aitken's Δ² process:

$S_n^{\prime}=S_{n+1}-\frac{(\Delta S_n)^2}{\Delta^2 S_n}$

and its generalization the Wynn ε algorithm:

$\varepsilon_{k+1}^{(n)}=\varepsilon_{k-1}^{(n+1)}+\frac1{\varepsilon_{k}^{(n+1)}-\varepsilon_{k}^{(n)}}$

for the latter one especially because it is nicely represented as a lozenge diagram:

Answer 61

I like Riemann-Roch the most!!!

Answer 62

polynomially convex hull of K = plurisubharmonic hull of K , where K is compact subset of C^n. For n>1, the equality is very interesting.