This post makes a focus on a very specific part of that long post. Consider the following map:
$$f: n \mapsto \left\{
\begin{array}{ll}
\left \lfloor{n/\sqrt{2}} \right \rfloor & \text{ if } n \text{ even,} \\
\left \lfloor{n\sqrt{2}} \right \rfloor & \text{ if } n \text{ odd.}
\end{array}
\right.$$
Let $f^{\circ (r+1)}:=f \circ f^{\circ r}$, consider the orbit of $n=73$ for iterations of $f$, i.e. the sequence $f^{\circ r}(73)$: $$73, 103, 145, 205, 289, 408, 288, 203, 287, 405, 572, 404, 285, 403, 569, 804, 568, 401, \dots$$
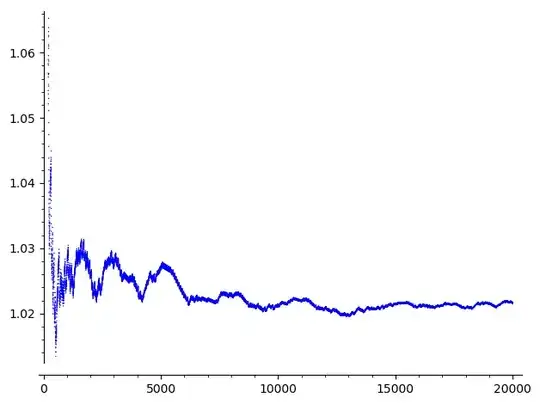
It seems that this sequence diverges to infinity exponentially, and in particular, never reaches a cycle. Let illustrate that with the following picture of $(f^{\circ r}(73))^{1/r}$, with $200<r<20000$:
According to the above picture, it seems that $f^{\circ r}(73) \sim \delta^r$ with $\delta \sim 1.02$.
Now consider the probability of the $m$ first terms of the sequence $f^{\circ r}(73)$ to be even: $$p_{0}(m):= \frac{|\{ r<m \ | \ f^{\circ r}(73) \text{ is even}\}|}{m}.$$ Then $p_1(m):=1-p_0(m)$ is the probability of the $m$ first terms of $f^{\circ r}(73)$ to be odd.
If we compute the values of $p_i(m)$ for $m=10^{\ell}$, $\ell=1,\dots, 5$, we get something unexpected: $$\scriptsize{ \begin{array}{c|c} \ell & p_0(10^{\ell}) &p_1(10^{\ell}) \newline \hline 1 &0.2&0.8 \newline \hline 2 &0.45&0.55 \newline \hline 3 &0.467&0.533 \newline \hline 4 &0.4700&0.5300 \newline \hline 5 &0.46410&0.53590 \newline \hline 6 & 0.465476& 0.534524 \end{array} }$$ (the line for $\ell = 6$ was computed by Gottfried Helms, see the comments)
It is unexpected because it seems that $p_0(m)$ does not converge to $1/2$, but to $\alpha \sim 0.465$.
It matches with the above observation because $$ \delta \sim 1.02 \sim \sqrt{2}^{(0.535-0.465)} = \sqrt{2}^{(1-2 \times 0.465)} \sim \sqrt{2}^{(1-2\alpha)}.$$
Question: Is it true that $f^{\circ r}(73)$ never reach a cycle, that $(f^{\circ r}(73))^{1/r}$ converges to $\delta \sim 1.02$, that $p_0(m)$ converges to $\alpha \sim 0.465$, and that $\delta^24^{\alpha} = 2$? What are the exact values of $\delta$ and $\alpha$? (or better approximations?)
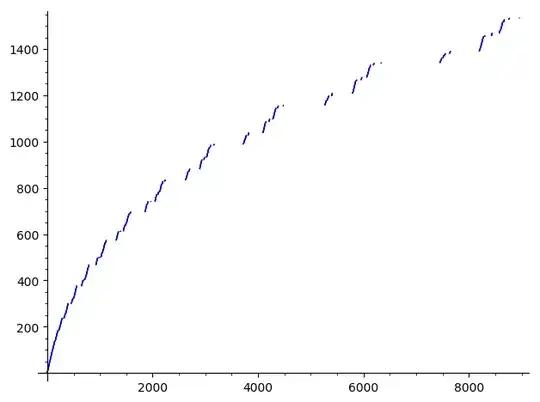
The following picture provides the values of $p_0(m)$ for $100 < m < 20000$:
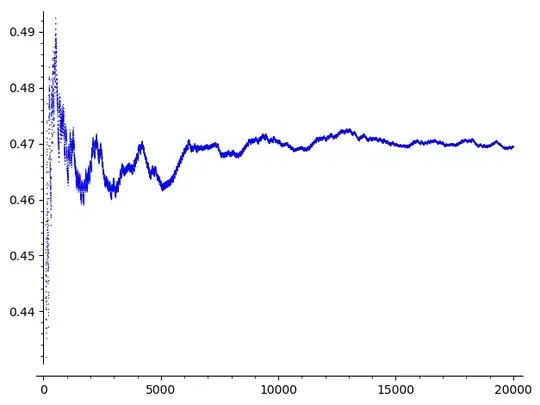
Note that this phenomenon is not specific to $n=73$, but seems to happen as frequently as $n$ is big, and then, the analogous probability seems to converge to the same $\alpha$. If $n <100$, then it happens for $n=73$ only, but for $n<200$, it happens for $n=73, 103, 104, 105, 107, 141, 145, 146, 147, $ $ 148, 149, 151, 152, 153, 155, 161, 175, 199$; and for $10000 \le n < 11000$, to exactly $954$ ones.
Below is the picture as above but for $n=123456789$:
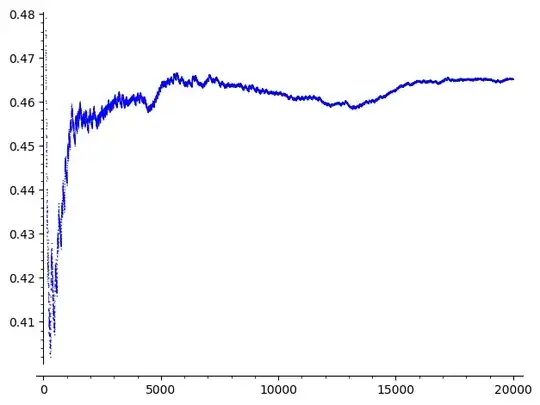
Alternative question: Is it true that the set of $n$ for which the above phenomenon happens has natural density one? Is it cofinite? When it happens, does it involves the same constant $\alpha$?
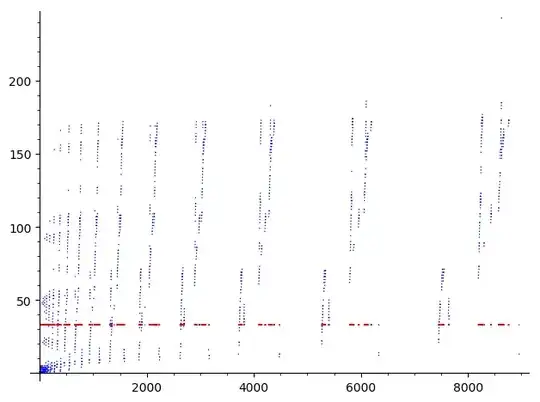
There are exactly $1535$ numbers $n<10000$ for which the above phenomenon does not happen. The next picture displays for such $n$ the minimal $m$ (in blue) such that $f^{\circ m}(n) = f^{\circ (m+r)}(n)$ for some $r>0$, together with the miniman such $r$ (in red):
In fact all these numbers (as first terms) reach the following cycle of length $33$:
$$(15,21,29,41,57,80,56,39,55,77,108,76,53,74,52,36,25,35,49,69,97,137,193,272,192,135,190,134,94,66,46,32,22)$$
except the following ones: $$7, 8, 9, 10, 12, 13, 14, 18, 19, 20, 26, 27, 28, 38, 40, 54,$$ which reach $(5,7,9,12,8)$, and that ones $1, 2, 3, 4, 6$ which reach $(1)$, and $f(0)=0$.
If the pattern continues like above up to infinity, they must have infinity many such $n$.
Bonus question: Are there infinitely many $n$ reaching a cycle? Do they all reach the above cycle of length $33$ (except the few ones mentioned above)? What is the formula of these numbers $n$?
f[n_]:=Floor[2^Mod[n,2] n/Sqrt[2]]on Mathematica I get for $f^{\circ2584}(73)$ the value$$670900640024419955928600637257.$$This is almost half of your value but not quite:$$1341801280048839911857201274496/2=670900640024419955928600637248$$ – მამუკა ჯიბლაძე Feb 26 '20 at 08:43Now I see that this $\beta$ is after all not that much smaller than $\sqrt2$, but it does seem to slowly decrease. Till where?? – Wolfgang Feb 27 '20 at 10:13