15

I would like to write an article about powerful existence theorems that assert, under mild and simple conditions, that some basic pattern or regularity exist. See some examples below. By mild conditions I mean short, easy, general. By simple conditions I mean that they should be accessible to undergraduate mathematics/science students.

I am especially interested in "low-dimensional" examples which allow an easy graphical representation.

I had some obvious examples in mind (given below), but many of them are rather classical results established until around 1970, roughly speaking.

I would be interested in more recent results. Thanks to the users that added great examples in the comments!

(1) Cantor Set, and existence of cardinalities $>|\mathbb N |$

(2) Lemma of Sperner, and Brouwer Fixed Point Theorem

(3) Lemma of Tucker, and Borsuk-Ulam Theorem

(4) Ramsey's Theorem

(5) Wallpaper Groups: There exist exactly 17 plane symmetry groups

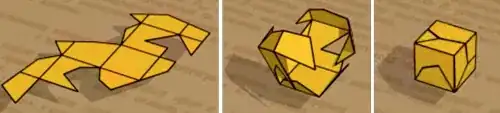
(6) Banach-Tarski Paradox

(7) Wagner's Theorem about Planar Graphs

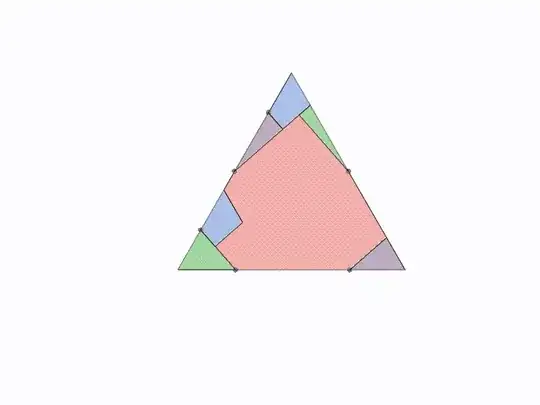
(8) Monsky's Theorem

(9) Four Color Theorem

(10) Penrose Tiling

EDIT: adding great examples from the comments

(11) Max-Flow Min-Cut Theorem from graph theory

(12) Tverberg's Theorem about intersecting convex hulls

(13) Van der Waerden's Theorem

(14) Szemerédi's Regularity Lemma from extremal graph theory

(15) Recent results about Existence of Designs (Keevash 2014, Glock et al. 2016)

Claus
  • 6,777
  • 3
    On the topic of Ramsey's theorem, you might be interested in van der Waerden's Theorem about arithmetic progressions. – Carl-Fredrik Nyberg Brodda May 17 '20 at 11:07
  • @Carl-Fredrik Nyberg Brodda, thank you very much. That is a great comment and reference! – Claus May 17 '20 at 11:35
  • 3
    The Max-flow Min-cut theorem was proved by Ford and Fulkerson in 1956, which is slightly later than 1950. – Sam Hopkins May 17 '20 at 13:14
  • @Sam Hopkins, thanks a lot for your comment! This is a great example and I will add as well. – Claus May 17 '20 at 13:40
  • 2
    I’m not sure what you mean by minimum regular pattern, but probably the existence of designs fits the bill (recent result of Keevash and of Glock et al). – user36212 May 17 '20 at 16:37
  • @user36212, thanks a lot for your comment! Very much appreciated. I will take a look at your reference, very interested in that. – Claus May 17 '20 at 17:04
  • 1
    Tverberg's theorem might be suitable, and its topological version also. – Geva Yashfe May 18 '20 at 09:52
  • @gyashfe, thanks a lot for this comment, you make a great point. I will add this one as well – Claus May 18 '20 at 10:33
  • 1
    Maybe: Infinite Ramsey theorem (from which the finite version follows). Also Szemerédi's regularity lemma. – LeechLattice May 18 '20 at 10:46
  • 1
    Would the recent breakthroughs in bounded gaps between primes qualify? The hypotheses are mild indeed (the basic necessary conditions), and the conclusion is remarkable. – Stanley Yao Xiao May 18 '20 at 11:22
  • @LeechLattice, thanks a lot for your great suggestion! I added to the examples in my question – Claus May 18 '20 at 12:02
  • @StanleyYaoXiao, great to have an example from number theory as well! Thanks a lot for your great comment – Claus May 18 '20 at 12:03
  • 1
    I don't really see how the twin primes example is supposed to qualify as an example of what the OP wants. But in the field of arithmetic combinatorics, Szemerédi's theorem- not the regularity lemma (which was developed to prove this theorem), but the one extending Roth's theorem- does seem to fit the bill. – Sam Hopkins May 18 '20 at 16:13
  • @SamHopkins, thanks a lot for your clarifying comment. I included Szeméredi's Theorem now in combination with Van der Waerden's earlier result. – Claus May 18 '20 at 17:22
  • 1
    Some of the answers to A search for theorems which appear to have very few, if any hypotheses might qualify. – Dave L Renfro May 18 '20 at 17:29
  • @DaveLRenfro, thanks a lot for this link, it is super helpful. – Claus May 18 '20 at 17:46
  • 2
    Brenier’s Theorem on the existence of transport maps between probability measures seems to qualify. – Alf May 19 '20 at 02:11
  • @Jon, Thanks a lot Jon for this great suggestion, it clearly qualifies. Based on your comment I read an article and this is a good example of what I am looking for. I will include your example in the list in my answer below – Claus May 19 '20 at 05:29
  • 1
    Monsky's Theorem does not seem like an existence theorem to me. It says that for all dissections of square into equal area subtriangles, the number of such triangles is even. Well, alright, to say that a number is even is an existence statement... but... – Lee Mosher May 23 '20 at 20:40
  • @LeeMosher it is a fair point and MattF made it as well. The way I read Monsky’s is that it asserts that a minimal regularity exists. – Claus May 23 '20 at 21:11
  • 1
    Not at all recent, but: on a smooth cubic surface lie exactly 27 lines. Many results from enumerative geometry have general position hypothesis or more complex conditions, but this is so simple to be striking – Andrea Ferretti Jun 11 '20 at 18:37

5 Answers5

17

Alexandrov's gluing theorem: If one glues polygons together along their boundaries to form a closed surface homeomorphic to a sphere, such that no point has more than $2\pi$ incident surface angle, then the result is isometric to a convex polyhedron, uniquely determined up to rigid motions.

There is as yet no effective procedure to actually construct the polyhedron guaranteed to exist.

A.D. Alexandrov. Convex Polyhedra. Springer-Verlag, Berlin, 2005. Monographs in Mathematics. Translation of the 1950 Russian ed. by N. S. Dairbekov, S.S. Kutateladze, and A.B. Sossinsky. p.100.

The result also holds for a single polygon, whose perimeter is glued closed by identifications:
          CubeMeta
          Snapshots from a video by Erik Demaine, Martin Demaine, Anna Lubiw, J.O'Rourke, Irena Pashchenko.
Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • 4
    I think you want to say "then the result is isometric to a convex polyhedron". Consider the cube on $(\pm1,\pm1,\pm1)$, with the top face replaced by four triangles going to $(0,0,1/2)$. Those instructions for gluing do not result in a convex polyhedron, but the result is isometric to the cube with the top face replaced by four triangles going to $(0,0,3/2)$, and that is a convex shape. –  May 18 '20 at 16:53
  • 2
    @Joseph O'Rourke, thanks a lot, this is a great example of what I am looking for – Claus May 18 '20 at 17:00
  • 2
    @MattF. Thanks for the correction. Among the class of convex polyhedra, the result is unique. Your phrasing is clearer, and I've changed it. – Joseph O'Rourke May 18 '20 at 17:18
9

There are a number of easily stated problems in elementary computational geometry that have been solved only relatively recently, e.g.,

  • the origami existence theorem that a single rectangular sheet of paper can be folded into the shape of any connected polygonal region, even if it has holes;

  • the fold-and-cut theorem that any shape with straight sides can be cut from a single sheet of paper by folding it flat and making a single straight complete cut;

  • the carpenter's rule problem of moving a simple planar polygon continuously to a position where all its vertices are in convex position, without ever crossing itself (below is an example from Erik Demaine's website);

  • the existence of hinged dissections; i.e., the existence of a common hinged dissection of any finite collection of polygons of equal area (below is an example due to Greg Frederickson).

Timothy Chow
  • 78,129
3

adding other great examples, many of them provided in the comments section

(16) Kakeya needle problem and Besicovitch sets: You want to rotate a needle of unit length by $360°$. What is the region with smallest area to do that? It turns out there is no lower bound > 0 for the area of such a region, i.e. you can find arbitrarily small such regions. (https://en.wikipedia.org/wiki/Kakeya_set)

(17) A more recent one, Brenier’s Theorem on the existence of optimal transport maps between probability measures. (https://en.wikipedia.org/wiki/Transportation_theory_(mathematics))

(18) Recent results about bounded gaps between primes (e.g. Zhang)

(Adding these examples as an answer because the list of examples in my original question is getting too long)

Claus
  • 6,777
  • @MattF., this is a fair comment and thank you for making it. I added it because of its extreme simplicity, and because it establishes what I would call a regularity: You can obviously divide it into an even number (=existence). But that's the only possible case and all other cases fail. I feel it draws a powerful and insightful line between existence and non-existence. – Claus May 18 '20 at 17:56
2

1) The set of continuous everywhere but differentiable nowhere functions on the unit interval is a meagre set of measure 1.

2) The existence of a space filling curve, or more generally surjective continuous maps $S^m \to S^n$ for $n>m$ (and then the fact that however any such map is homotopic to a map that misses a point).

E. KOW
  • 732
1

This example is not really recent, since it was discovered in 1849 by Cayley and Salmon, but I think it qualifies. On a smooth cubic surface in $\mathbb{CP}^3$ there are exactly 27 lines.

This is a prototypical result in enumerative geometry. There are plenty of results in the same spirit, such as the 3264 conics tangent to 5 general conics, or the (related) 28 bitangents to a general quartic curve, but I think that Cayley-Salmon is striking for the simplicity of its hypothesis.

Andrea Ferretti
  • 14,454
  • 13
  • 78
  • 111