This is a variation on a (much) earlier MO question, Hanging a ball with string. Here instead the task is to arrange a net of string to hang a unit cube. Assume:
- The string is inelastic.
- There is no friction between the string and the surface.
- There is an attachment point for attaching a vertical hanging string.
- The cube cannot "slip out" under small jostlings.
- The net has minimal total length among all such nets.
The aspect that I do not know how to formalize is slipping-out. Intuitively I want it to be robust under nudging. Formally there should be a requirement that the cube live in some positive radius ball in a configuration space such that within that ball, the cube remains confined by the net.
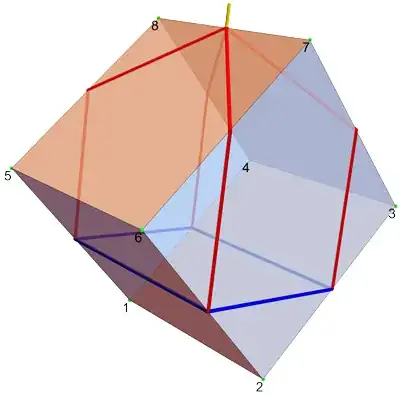
String length: $2+5\sqrt{2} \approx 9.07$ (excluding yellow piece).
I offer two nets as examples to improve. In the first above, the blue rectangle corners are at edge midpoints, and the four red paths to the attachment point are geodesics. This net seems to satisfy the no-slipping-out condition, and I have verified this is optimal among nets that slide the blue rectangle corners in concert up or down those cube edges. But many aspects are unclear. In particular:
Q1. Remove one red path, leaving the other three. Can the cube now slip out? Note the blue paths are not geodesics, in that they do not unfold straight around a corner.
There are six $\sqrt{5}$-geodesics between opposite cube corners $v_1$ and $v_7$. Choose four, perhaps those shown below; note that $4 \sqrt{5} \approx 8.94$ is slightly shorter than the first net above.
Q2. Does it avoid slipping-out? If so, can the net be reduced to three geodesics and still avoid slipping-out?

String length: $4 \sqrt{5} \approx 8.94$ (excluding yellow piece).
Q3. What is a more formal definition of the no-slipping-out condition that captures the intuition, and allows settling some of the questions above?
Of course the main question is: What is the minimum length net?