20

The "napkin-ring problem" sometimes shows up in 2nd-year calculus courses, but it can fit quite neatly into a high-school geometry course via Cavalieri's principle.

However, the conclusion remains astonishing. Is there some advanced viewpoint from which it becomes obvious from some sort of symmetry that's not visible in the naive formulation?

Steve Huntsman
  • 15,258
Michael Hardy
  • 11,922
  • 11
  • 81
  • 119
  • Perhaps one could use Pappus' theorem? (Although I think determining the center of mass of the solid of revolution might be more work than it's worth... – dvitek Aug 31 '10 at 21:17

5 Answers5

9

I think it's a bit more elegant to use a different version of Cavalieri's principle: instead of taking cross-sections, sweep the napkin ring by half-disks, bounded by semicircles on the outer sphere whose diameter is the same as the napkin ring's height. The shape of the half-disk is independent of the outer radius. The instantaneous volume swept by the half-disk, per unit angle, just looks (in the limit as the angle goes to zero) as a wedge of a sphere, so it's also independent from the outer radius.

Edited to add: I think this is the argument in the following reference from the Wikipedia article: Levi, Mark (2009), "6.3 How Much Gold Is in a Wedding Ring?", The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press, pp. 102–104, ISBN 978-0-691-14020-9.

David Eppstein
  • 18,497
  • @David: May I ask you to explain the sweep more precisely? Are the half-disks swept parallel to themselves, or are they rotating on a fixed diameter? Perhaps I am having difficulty with the phrase "bounded by semicircles on the outer sphere," but I am not seeing the picture you are painting. No doubt my fault... – Joseph O'Rourke Aug 31 '10 at 22:46
  • To speak of "the outer sphere" seems to presuppose that one sphere is inside another, so the latter is "the outer sphere". Is that what you meant?

    It took me a while to reach the point where I felt I knew what you're (probably?) saying. If I were going to present it to a class of high-school students, I'd expect them to find the version in the Wikipedia article clearer.

     – Michael Hardy Aug 31 '10 at 23:53
  • You wrote "The shape of the half-disk is independent of the outer radius." Could it be that you meant "The size of the half-disk is independent of the outer radius."? – Michael Hardy Aug 31 '10 at 23:54
  • Draw a stick connecting the center of the sphere to a point halfway from top to bottom on the inner surface of the hole. Attach the disk perpendicularly to the stick. Rotate the stick around the equator keeping the disk attached to it.

    By "the outer sphere" I mean the sphere that the hole is drilled through.

    By "the shape of the half-disk is independent" I meant, up to congruence. Obviously all half-disks have the same shape up to similarity.

     – David Eppstein Sep 01 '10 at 00:40
  • Even after all the clarifications, I have a hard time understanding why is the instantaneous volume a spherical wedge, since both the diameter of the half-disk and the plane of the disk are rotated simultaneously. – Victor Protsak Sep 01 '10 at 08:07
  • 1
    The instantaneous movement of the center of the disk is parallel to the disk and doesn't affect it's volume. The only remaining component of the instantaneous motion is the rotation of the plane of the disk, and that's the only component that affects the volume, but it only depends on the turning angle and not the sphere radius. – David Eppstein Sep 01 '10 at 15:23
  • @David: Of course all half-disks have the same shape, but isn't the relevant fact here that in this case they have the same size? – Michael Hardy Sep 01 '10 at 17:08
  • @David, Beautiful construction! @Victor, take the limit as $\Delta \theta \to 0$, for either David's construction illustrated above, or for the volume of a sphere of radius $h$

    $$V=\int_{\theta=0}^{\theta=2\pi} \frac{1}{2}\pi r^2$$

    and notice that when the integration is done over the angle $\theta$, then the inner radius does not play a role in the integration.

     – sleepless in beantown Sep 01 '10 at 17:27
  • The half-disc of radius $h$ is the limiting area swept per $d\theta$ in both the sphere of radius $r$ and in David Eppstein's elegant construction. – sleepless in beantown Sep 01 '10 at 17:29
  • Of course, if you really wanted to know how much gold is in a wedding ring, you might start by doing the two things Archimedes did: weight it, and see how much water it displaces. – Michael Hardy Sep 01 '10 at 22:24
  • 1
    This is a really nice argument. So if I understand correctly, instead of a circle, one could take any smooth simple closed curve whose tangent vector rotates monotonically, and sweep out a solid by sliding a semicircular disk around the curve, always keeping the semicircular disk perpendicular to the plane of the curve and in the plane of the tangent vector. – Timothy Chow Sep 30 '13 at 22:47
7

This is my attempt to understand David Eppstein's construction. The green segment is the "stick connecting the center of the sphere to a point halfway from top to bottom on the inner surface of the hole." The half-disk that gets angularly swept around the center of the sphere is purple. The napkin ring ("hole") is red.

Edit. Altered as per David's comment.

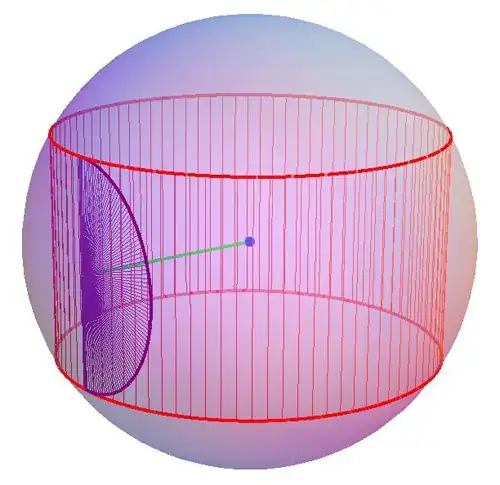
alt text

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
2

EDIT: More briefly than before . Here is a naive physical argument which might meet the request of a point of view from which the result would immediately appear to be just what one would expect before going through the argument.

  • A blob of (incompressible) fluid volume V will form a spherical ball of radius (what it needs to be) if uncontrained
  • A blob of fluid volume V constrained between two parallel plates at z=r and z=-r will form the height 2r central slice of a sphere of radius R where R is just right so that the slice has volume V (provided r is not too large relative to V in which case we get a sphere)
  • A blob of fluid of volume V constrained between two parallel plates at z=r and z=-r and with a cylinder of height 2r and radius q imposed in the middle will form (along with the cylinder) the height 2r central slice of a sphere of radius R where R is just right so that the slice has volume $V+\pi q^2 h$. This shape might not have the curved boundry reach the cylinder
  • Imagine that the volume is just right to get that napkin ring. Now start shrinking q. We will still have a napkin ring. Keep going until q=0 and we see that the volume was that of a sphere of radius r.

(read the previous version if you wish, it might not be worth it)

Aaron Meyerowitz
  • 30,015
  • I'm going to have to think about this one.....

    If this works, it seems to me that essentially the same reasoning could work for other geometric problems, even though I don't know right now what those would be.

     – Michael Hardy Sep 05 '10 at 00:52
  • I think I might have seen it in vol 1 of Mathematics and Plausible reasoning by George Polya. A similar result holds for paraboloids and other conics as I recall. I suppose a cone is easy (given the cylinder) since it has the same volume as the cylinder meeting its equator. – Aaron Meyerowitz Sep 05 '10 at 20:09
1

Let $V(r,z)$ denote the volume of a napkin ring of outer radius $r$ and height $2z$. We have that $V(r,rz) = r^3 V(1,z)$ and $V(1,az) = a^3 V(1,z)$. The former equality is trivial. To see the latter one, note that $V(1,z) = 4\pi z^3/3$.*

It follows that $V(r,z) = r^3 V(1,r^{-1}z) = r^3 r^{-3} V(1,z) = V(1,z)$.

*This might want some fleshing out: e.g. decomposing the complementary part of the sphere into two spherical cones, a cylinder, and two "negative" cones. The volumes of the cylinder and cones can be trivially computed; the volume of a spherical cone can be computed without calculus using its solid angle $\Omega$ and taking the proportion $\Omega/4\pi$.

Steve Huntsman
  • 15,258
  • Your identities are certainly correct, but it doesn't seem to address the second paragraph of my question, any more than the argument from Cavalieri's principle does. – Michael Hardy Sep 01 '10 at 00:31
  • I'm not following your proposed decomposition of the complementary part of the sphere. Can you explain that a bit more long-windedly? – Michael Hardy Sep 01 '10 at 00:32
  • OK, the volume of the complementary part of the unit sphere is $V_c(z) = 2S(z)+2\pi(1-z^2)z-2\pi(1-z^2)z/3$, where the terms correspond to the two spherical cones, the cylinder, and the "negative" cones, respectively. The solid angle of each spherical cone is $\Omega = 2\pi(1-z)$, so $2S(z) = (4\pi/3)(1-z)$ and $V_c(z) = 4\pi(1-z^3)/3$. Now $V(1,z) = 4\pi/3 - V_c(z) = 4\pi z^3/3$. As to how advanced this is, well I don't think it's advanced at all. But it is a manifest expression of scaling symmetry. – Steve Huntsman Sep 01 '10 at 02:13
  • I've neglected this thread for a while; maybe I look it over again today or tomorrow....... – Michael Hardy Sep 17 '10 at 12:38
  • @MichaelHardy Dear Sir, I know You four year ago on wiki, now this theorem have 9 cite publish in 5 Journals. Can You convert to en.wiki

    See also:

    https://mathoverflow.net/questions/234053/daos-theorem-on-six-circumcenters-associated-with-a-cyclic-hexagon

     – Đào Thanh Oai Jun 29 '18 at 03:37
  • @MichaelHardy Dear Sir, I know You four year ago on wiki, now this theorem have 9 cite publish in 5 Journals. Can You convert to en.wiki

    See also:

    https://mathoverflow.net/questions/234053/daos-theorem-on-six-circumcenters-associated-with-a-cyclic-hexagon

     – Đào Thanh Oai Jun 29 '18 at 03:37
1

The key in seeing this lies in breaking it down into a series of stacked washers or discs.

  • Define the napkin ring of height $h$ as being hollowed out of a sphere of radius centered at the origin with radius $R=\alpha h$, with $\alpha\ge1$

  • Define the hole as being drilled along the $z$-axis, creating the napkin ring with an outer diameter $r_\text{out}$ and inner diameter $r_\text{in}$ defined as functions of $z$.

  • $r_\text{out}=\sqrt{R^2-z^2}$ and inner diameter $r_\text{in}=\sqrt{R^2-(h/2)^2}$

  • Define the volume as the integral over $z$ ranging over ($-h/2, +h/2$)

$$\pi \int_{-h/2}^{h/2} (r_\text{out}^2-r_\text{in}^2) \, dz$$

as the volume being height ($dz$) multiplied by the area ($\pi r_\text{out}^2 - \pi r_\text{in}^2)$ of the outer disk minus the inner disk. Note that the $R^2$ cancels out, showing that the radius of the sphere of material does not affect the AREA of the annulus at height $z$.

This is the intuitive step that may be hard to grasp. The thickness of the napkin ring ($r_\text{out}-r_\text{in}$) certainly does change with the radius $R$ of the carving sphere. As $R$ increases, the thickness of the napkin ring decreases inversely proportional to the square of $R$. This inverse relationship is what keeps the areas of the annuli at height $z$ at a value that is independent of $R$.

The intuitive mis-step is in thinking that even as $R$ increases, the thickness of the napkin ring stays the same. This is incorrect. A similar intuitive mis-step also occurs with this example.

You are wearing a belt of circumference 1 meter. You let out the belt ~31.416 centimeters (~ ten belt notches). How far over your body will the belt float? (also, how much larger can you now become?) The answer is 10 centimeter increase in radius.

The earth is wearing a belt at its equator of circumference $C$. How much do you have to let the belt out to create a an increase in radius of 10 centimeters for the earth? The answer is the same $\sim31.416$ centimeters, since circumference is linearly proportional to radius. $C=2\pi r$

In the napkin ring problem, the key is that the area of the annuslus as a function of distance along the longitudinal-axis remains constant despite any change in $R$ because of the inverse-square proportionality. Intuition fools us into thinking that the thickness must remain constant for such a thing.

Michael Hardy
  • 11,922
  • 11
  • 81
  • 119
sleepless in beantown
  • 2,391