Given a positive integer $n$, some straight lines and lattice points such... Prove that the number of the lines is at least $n(n+3)$

Question

I was trying to get an answer on MathSE long ago and now I got it.

Given a positive integer $n$ and some straight lines in the plane such that none of the lines passes through $(0,0)$, and such that every lattice point $(a,b)$, where $ 0\leq a,b\leq n$ are integers and $a+b>0$, is contained by at least $a+b+1$ of the lines. Prove that the number of the lines is at least $n(n+3)$.

Solution: Let us count the number of pairs $({\bf line},{\bf point})$ on two ways.

• Say we have $l$ lines and each can pass at most $n+1$ points. Say $k$ of them pass through $n+1$ points, then $k\leq 2n+1$. So all of them pass at most through $$k(n+1)+n(l-k) \leq (l+2)n+1$$ points, so we have at most $(l+2)n+1$ pairs $({\bf line},{\bf point})$.
• On the other hand all points pass at least thorugh $$\sum_{a=0}^n\sum_{b=0}^n (a+b+1)-1 = n^3+3n^2+3n $$ lines, so we have at list that many pairs $({\bf line},{\bf point})$.
• So we have $$n^3+3n^2+3n\leq (l+2)n+1\implies l\geq n(n+3)$$ and thus a conclusion.

Is there a polynomial method aproach to this problem? (Like defining some polynomials which wanish on some set of points...)

Answer 1

With polynomial method you may prove the same bound even if the lines are allowed to coincide. Then it is sharp: consider the vertical and horizontal lines $x=a$ and $y=a$ taken $a+1$ times for $a=1,2,\ldots,n$. Also it works over any field (and with points $(\alpha_i,\beta_j)$ on the place of $(i,j)$, where $\{\alpha_0,\ldots,\alpha_n\}$ and $\{\beta_0,\ldots,\beta_n\}$ are arbitrary subsets of the field.)

For the proof, we adapt the standard Alon -- Furedi trick for the multisets. Namely, we use the multisets analogue of this formula.

If $A\subset \mathbb{R}$ is a multiset, denote by $n(a)$ the multiplicity of the element $a$ in $A$. If $f(x)\in \mathbb{R}[x]$ is a polynomial, we say ``the values of $f$ on $A$'' for the sequence of numbers $f^{(i)}(a)$, where $a\in A$ and $0\leqslant i\leqslant n(a)-1$. It is well known that if $\deg f\leqslant |A|-1$, $f$ is uniquely determined by its values on $A$ (Hermite interpolation). In particular, the coefficient $[x^{|A|-1}] f(x)$ may be written in the form $\Phi_A(f)$, where $\Phi_A$ is a linear combination of the values of $f$ on $A$.

Remark. Whenever $n(a)=1$, the value $f(a)$ participates in $\Phi_A$ non-trivially. This follows from considering the sample polynomial $f(x):=\prod_{b\in A\setminus a} (x-b)^{n(b)}$.

Now if we have two multisets $A,B\subset \mathbb{R}$ and the polynomial $f(x,y)$ such that $\deg f\leqslant |A|+|B|-2$, we may write the formula $$\left[x^{|A|-1}y^{|B|-1}\right]f=\left(\Phi_A\otimes \Phi_B\right) f(x,y).\quad\quad\quad(1)$$ Here we identify the space of polynomials in $(x,y)$ with the tensor product of polynomials in $x$ and polynomials in $y$. So, (1) allows to reconstruct the coefficient of $x^{|A|-1}y^{|B|-1}$ in the polynomial $f$ via the values $((\partial/\partial x)^i (\partial/\partial y)^j f)(a,b)$, $a\in A$, $b\in B$, $i$, $j$ are less then corresponding multiplicities of $a$ in $A$ and $b$ in $B$. The coefficient of such guy is a product of corresponding coefficients for 1-dimensional reconstruction formulae.

Once stated, (1) is easy to prove: by linearity, we may think that $f(x,y)=x^k y^l$, $k+l\leqslant |A|+|B|-2$. Then RHS of (1) reads as $\Phi_A(x^k) \Phi_B(y^l)$. If both $k\leqslant |A|-1$, $l\leqslant |B|-1$, we may use the 1-dimensional formulae $\Phi_A(x^k)=[x^{|A|-1}]x^k$, $\Phi_B(y^l)=[y^{|B|-1}]y^l$. If, say, $k\geqslant |A|$, the 1-dimensional formula is no longer valid for $x^k$, but we have $l<|B|-1$, and for $y^l$ the formula $\Phi_B(y^l)=[y^{|B|-1}]y^l$ is valid and gives 0. Cause of this 0, it does not really matter what is the value $\Phi_A(x^k)$.

Well, now back to the problem. Assume that we have less than $n(n+3)$ lines. Take the product of their equations, it is a polynomial $f(x,y)$ of degree less than $n(n+3)$. Consider the multisets $A=B=\{0,1,1,2,2,2,\ldots,n,\ldots,n\}$, $|A|=n(n+3)/2+1$. We have $\deg f<|A|+|B|-2$, thus $[x^{|A|-1}y^{|B|-1}]f=0$. But applying (1) we see that there is unique non-zero term in RHS, which corresponds to $f(0,0)$: all other terms have the form $((\partial/\partial x)^i (\partial/\partial y)^j f)(a,b)$, $(a,b)\ne (0,0)$, $i\leqslant a,j\leqslant b$, they do vanish because of the multiplicity condition. The term $f(0,0)$ goes with non-zero coefficient due to Remark. A contradiction.

You may read more about this multisets formula in [G. Károlyi, Z.-L. Nagy, F. V. Petrov, V. Volkov. A new approach to constant term identities and Selberg-type integrals. Adv. Math. 277 (2015), 252-282], earlier the tensor product view appeared in [U. Schauz. Algebraically solvable problems: describing polynomials as equivalent to explicit solutions. Electron. J. Combin. 15 (2008) #R10, 35 p.]

---

When the lines are all distinct, this seems to be too weak bound, let me prove $\Omega(n^{5/2})$.

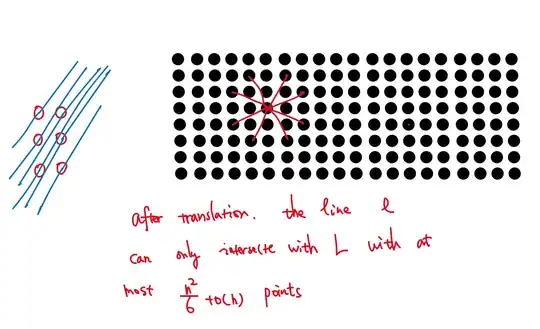
If a point is covered by a line, draw a flower at this place. The number of flowers should be at least $cn^3$ for some $c>0$. On the other hand, denote by $r_k$ the number of lines containing at least $k$ points. The vector between consecutive lattice points on such line may be chosen by $O(n^2/k^2)$ ways, the line should pass through a point which may be chosen by $O(n^2)$ ways, and each such line is counted at least $k$ times, totally we get $r_k\leqslant С n^4/k^3$ for certain $C$. Choose large $M$ and consider only $k\geqslant M\sqrt{n}$. We get $\sum_{k\geqslant M\sqrt{n}} r_k\leqslant Cn^4/(M^2n)=(C/M^2)n^3<cn^3/2$ if $M$ is large enough. This means that if label only $\max(s,[M\sqrt{n}])$ flowers corresponding to each line containing exactly $s$ points, the total number $\sum_{k> M\sqrt{n}} r_k$ of not-labelled flowers is at most $cn^3/2$. All other $cn^3/2$ flowers are labelled, and each line contains at most $M\sqrt{n}$ labelled flowers. Thus the number of lines is not less then $\frac{c}{2M} n^{5/2}$.

Answer 2

You can get a better bound with a simpler proof.
Consider only the $n+1$ points for which $b=n$.
There is at most one line that goes through at least two of these points.
Thus any point $(a,n)$ has at least $a+n+1-1=a+n$ lines that go through only it from among these points.
So just through these points we have at least $$1+\sum_{a=0}^n (a+n)=1+n+(n+1)+...+(2n)=\frac{3n(n+1)}2+1$$ lines.

Answer 3

When the lines are all distinct it seems to be too weak bound as mentioned previously by Fedor Petrov.

let me prove for $n$ suffice large, the number of distinct lines we need to fill the lattice $L$, i.e. s.t. $\forall 0\leqslant a,b\leqslant n, 1<a+b$, $(a,b)$ is contained in at least $a+b+1$ of lines is $\Omega\left(n^{5/2} /(\ln n)^{2}\right)$. This is weaker than Fedor Petrov's result, and it is a prove without involve polynomial method.

the main argument is a mix of rearrangement inequality and mean value estimate for divisor function $d(n)=\sum_{d|n} 1$.

let $L=\{(a, b) \mid 0\leqslant a, b \leqslant n, a,b\in \mathbb{Z}\}$ be the lattice. $\#A$ is the number of elements in $A$.

Remark: $L$ is not the lattice in the normal definition of mathematics, but let us call it lattice because it is very visualizable.

---

First let us estimate $$\quad \#\{l \mid l \cap L=\frac{n}{k}\}\quad \quad (*)$$

$l$ runc in all the line in plane $\mathbb R^2$, and here the mean of $l \cap L=\frac{n}{k}$ is after some translation $T$ in translation group, $\# T(l)\cap L=\frac{n}{k}+o(n)$

In fact, $$ \#\left\{l \mid l \cap L = \frac{n}{k}\right\} = 4\left(\sum_{d_1 d_2=k} d_{1} d_{2}\right)n\leqslant 4d(k)kn\quad\quad (**) $$

---

$(**)$ is wrong and it should be** $ \#\left\{l \mid l \cap L = \frac{n}{k}\right\} = \frac{4\left(\sum_{d_1 d_2=k} d_{1} d_{2}\right)n}{n/k}=4d(k)k^2n $, I will fix the following argument use this later.

---

and $$\#\left\{l \mid l \cap L = \frac{n}{k}\right\}=O(d(k)kn)$$

Remark: $4$ is the number of elements of the unity group $\{1,-1,i,-i\}$

---

Now. if $\bigcup_{i \in I} I_{i}$ fill the lattice $L$ s.t. $\forall a+b>0$ $(a,b)\subset \mathbb Z^2$ is contained in at least $a+b+1$ of lines.

Then $$ \sum_{i \in I} \# l_{i} \geqslant n^{3}+3 n^{2}+3 n\geqslant n^{3} $$

And by rearrangement inequality,

$$ \sum_{i \in I}\# l_{i}\leqslant\sum_{s=1}^{M} \sum_{l_i, \# l_{i} = \frac{n}{s}} \# l_{i}=\sum_{s=1}^{M} \frac{n}{s} \cdot \#\left\{l \mid \# l\cap L = \frac{n}{s}\right\}. $$

Where $\sum_{s=1}^{M-1} \{l_i|\# l_{i}=\frac{n}{s}\}\leq \# I \leq \sum_{s=1}^M \{l_i|\# l_{i}=\frac{n}{s}\}$ and by $(**)$ we know,

$$ \sum_{s=1}^{M} \frac{n}{s} \cdot \#\left\{l \mid \# l \cap L=\frac{n}{s}\right\} \leqslant \sum_{s=1}^{M} \frac{n}{s}\cdot 4d(s)sn=\sum_{s=1}^{M}4d(s)n^2$$

So $$\sum_{s=1}^{M} 4 d(s) n^{2} \geqslant n^{3}, \ so, \sum_{s=1}^{M} d(s) \geqslant n$$

---

From the Fourier series of the Eisenstein series and the invariants of the Weierstrass elliptic functions, see this, we know,

$$\sigma_{k}(n)=\zeta(k+1) n^{k} \sum_{m=1}^{\infty} \frac{c_{m}(n)}{m^{k+1}}$$ in particular we know,

$$d(n)=\sigma_{0}(n)=\zeta(1) \sum_{m=1}^{\infty} \frac{c_{m}(n)}{m}$$

so $\sum_{n<x}d(x)\sim x\ln x$, so for $n$ suffice large and $\epsilon>0$, $\# I\geqslant \sum_{s=1}^{\frac{n}{\ln n}}4d(s)sn$ so $\# I= $\Omega\left(n^{5/2} /(\ln n)^{2}\right)$$.

Remark we can direct prove this, \begin{aligned} \sum_{n\leqslant x} d(n) &\left.=\sum_{n \leqslant x}\sum_{d|n}1\right. \ &=\sum_{d \leqslant x} \sum_{n \leqslant x, d|n} 1 \ &=\sum_{d \leqslant x}\left[\frac{x}{d}\right] \ &=\sum_{d \leqslant x}\left(\frac{x}{d}+o(1)\right) \ &=x \log x+O(x) \end{aligned}

---

Of course, there has some space to improve further, it seems very unlikely there is no cancellation when the distribution of $l$ in $I$ near the equal condition of rearrangement inequality because here I only use the $L_1$ norm of $L$ , but do not consider the shape of the function induce by lattice $L$, i.e. s.t. $\forall 0\leqslant a,b\leqslant n, 1<a+b$, $(a,b)$ is contained in at least $a+b+1$ of lines.

and a question is, is this method can generalize to finite field case? If it can it will be very interesting, I try to solve the finite field toy problem first and then use Fourier analysis on $(\mathbb Z/{p \mathbb Z})^2$ then find in the frequency space the problem is almost the same as the physics space and there is something look like to be very difficult this way I can not solve.

Let me give a picture to explain $(**)$