Deconvolution using the discrete Fourier transform

Question

Summary: From discrete convolution theorem, it is understandable that we need 2N-1 point DFT of both sequences in order to avoid circular convolution. If we need to do deconvolution of a given experimental M-point signal using the DFT, how do we avoid the circular effects. Do we still need to zero pad the signal to 2M-1 points for DFT deconvolution or not. Some sources say, without explanation, that zero padding is not needed in deconvolution.

It is a well known property of convolution, that convolution of two continuous functions is a multiplication in the frequency domain i.e., $y$ (t)= $a$ * $b$ becoming a multiplication after Fourier transform: F(y(t))= F( $a$ )F( $b$ ). This was well known by early 1900s and clearly mentioned in 1941 as discussed in previous questions here.

In practical applications, deconvolution is also desirable. In deconvolution, two functions are divided in the Fourier domain to recover the original function, say $a$ , if $y$ (t) and $b$ (t) are known. For example, if we wish to recover $a$ , we can divide F( $y$ (t)) by F( $b$ ) and do an inverse transform to get $a$ . It may not be a mathematically rigorous way, but it is a popular technique in spectroscopy from an empirical perspective.

In majority of the instrumental applications, the function is a discrete and problem is to perform deconvolution using Discrete Fourier Transform. Now the point is that in the DFT, the multiplication of the DFT of two functions yield a circular convolution, not a linear one.

However, one can extract the true linear convolution by ensuring that the length of the DFT equal to 2N-1, where N is the length of the data points contained in the discrete function.

Illustration Suppose $x_{1}=[\underline{1}, 2,3]$ and $x_{2}=[\underline{1}, 1,1] .$ We can compute the linear convolution as $x_{3}[n]=x_{1}[n] * x_{2}[n]=**[\underline{1}, 3,6,5,3]**$ If we instead compute $x_{3}[n]=\operatorname{IDFT}_{N}\left(\operatorname{DFT}_{N}\left(x_{1}[n]\right) \cdot \operatorname{DFT}_{N}\left(x_{2}[n]\right)\right)$ we get $x_{3}[n]=\left\{\begin{array}{ll} {[\underline{6}, 6,6]} & N=3 \\ {[\underline{4}, 3,6,5]} & N=4 \\ **{[\underline{1}, 3,6,5,3]} & N=5** \\ {[\underline{1}, 3,6,5,3,0]} & N=6 \end{array}\right.$

Linear convolution and DFT convolution match when the length of the DFT is at least 2N-1, which is 5 in this case.

Question: Do we need to apply the same length restriction of 2N-1 size of data when wish to divide in the frequency domain or not, in other words trying to do a linear deconvolution using DFT?

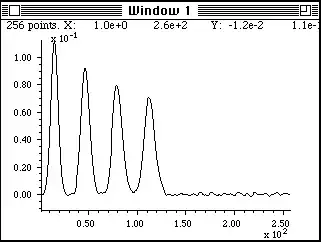
Suppose this is a observed sampled signal with 256 points (left, Window 1). We also know what distorted it by linear convolution. Its length was 256 points.

What people do is that they do a 256 point DFT on the observed signal. DFT is also performed on the distorted function, 256 points.

a) Divide the DFT(observed signal)/DFT(distorting function);

b) Take the inverse DFT, we get

I searched plenty of places, books and papers but could not find a clear requirement about the length of DFT in the case of division/deconvolution. Thanks

I'd suggest you stand back and look again at the problem from which this issue arises -- convolution is a smoothing operation, suppressing high frequencies, so deconvoluton will obviously amplify high frequencies, so (numerical or other) noise. The deconvolution problem is ill-posed so is typically attacked with methods of regularisation rather than a direct inversion. This probably accounts for the paucity of references to it you noted. — J.J. Green, Jan 15 '21 at 09:18
If I understand correctly, your question is: we know $x_3 = x_1 \star x_2$ (of length $n+k-1$ ) and $x_1$ (of length $n$ ), how do we find $x_2$ (of length $k$ ) using DFT. The answer is simple: pad your $x_1$ and $x_3$ with zeroes so that both have length $N \geqslant n + k - 1$ , calculate DFT, divide, calculate inverse DFT, and finally unpad (is that a word? Edit: is "trim" the right word?) to get $x_2$ . — Mateusz Kwaśnicki, Jan 15 '21 at 09:49
@MateuszKwaśnicki, This is exactly the problem I am exploring. But let us come to an experimental problem. Suppose we have an experimental data with 2000 points and we also know what caused the distortion in the signal by linear convolution. In order to do DFT based deconvolution, should one do a DFT deconvolution with 2*2000-1 or just 2000 points. — AChem, Jan 15 '21 at 14:35
If you know $x_3$ and $x_3$ has length $n+k-1 = 2000$ , then you are good to go with $N = 2000$ , why not. However, if you are working with real-life (inaccurate) data, then you should really stick to what J.J. Green wrote in his comment above. — Mateusz Kwaśnicki, Jan 15 '21 at 14:43
@MateuszKwaśnicki, I agree that DFT based deconvolution is not the perfect one but it is still very popular. Consider this as the experimental scenario. You will have an experimental data with N=2000, and a discrete "distorting function" which ruined the original signal by linear convolution, whose length is also N=2000. We wish to recover the true undistorted data. I think we should go for 22000-1 during DFT division* in order to do recover it by linear deconvolution not circular deconvolution. — AChem, Jan 15 '21 at 14:50
If the length of the original signal is equal to the length of the distorted one, then the distorting kernel must have had length one and there is nothing to do. Either I misunderstood what you wrote or your problem is not well-posed at all. — Mateusz Kwaśnicki, Jan 15 '21 at 14:52
May be I was not clear. Let me add a graphical version in the original question. A picture is worth a thousand words. — AChem, Jan 15 '21 at 15:08
Then, according to the picture, your distortion kernel has length approximately 60 (right-padded with zeroes), the original signal has approximately 130 points (right-padded with zeroes, up to numerical artifacts), and the distorted signal has length roughly 185 (right-padded with zeroes). This agrees with what I wrote above, does it not? — Mateusz Kwaśnicki, Jan 15 '21 at 15:59
@MateuszKwaśnicki, Right, your number analysis agrees with the n+k-1 requirement. However, if we assume that the original data had 130 points, then this will create experimental problems. For example, this implies that one collected the data up to 130 s (one point per second) rather than 256 seconds. In reality the signal was collected to for 256 s. In practice, I can tell you that people really do not care about this requirement n+k-1, but I am wondering why. They take the length of the distorting kernel same as the experimental signal, divide their DFTs and do an inverse. — AChem, Jan 15 '21 at 16:12

Carlo Beenakker · Answer 1 · 2021-01-17T22:18:24.537

3

If you work in the frequency domain there is no need to zero-pad the data to achieve a minimum length. In the time domain the resulting signal will then be periodically extended beyond the boundaries.

Perhaps this could be the "reputable source" requested in the update: Direct frequency-domain deconvolution when the signals have no spectral inverse --- [open access]

Section 4 gives the algorithm: the time-domain signals $h(n)$ and $y(n)$ of length $N$ are padded by zeros to length $2N$ , giving $h_1(n)$ and $y_1(n)$ . The Fourier transforms $Y_1(k)$ and $H_1(k)$ have length $2N$ , however, only the $N$ values at even $k$ are needed for the division/deconvolution.

So the algorithm requires a pair of $2N$ Fourier transforms but the inverse Fourier transform has length $N$ .

edited Jan 17 '21 at 22:18

answered Jan 15 '21 at 09:42

Carlo Beenakker

177,695

Thanks, Let us say, we have a single Lorentzian peak as a signal with 1024 points. When we wish to decrease its width, one can take the DFT of the signal we can divide it with the DFT of another Lorentzian of smaller width than the signal. It also needs 1024 points. The key point is do we need to do zero pad both to 2x1024 points? And after inverse we keep the first 1024 points. In reality, I see no difference with or without zero padding. – AChem Jan 17 '21 at 22:13
1

an alternative to zero-padding in the time domain is interpolation in the frequency domain, so there is no need to zero pad; zero-padding adds no new information, it is just an efficient way to interpolate the intermediate frequencies you want to use in order to avoid the circular convolution; you might find this discussion instructive. – Carlo Beenakker Jan 17 '21 at 22:27
I have been reading about zero padding, but nobody talks about it in the context of deconvolution using the DFT. From discrete convolution theorem, it is understandable that we need 2N-1 point DFT of both sequences in order to avoid circular convolution. If we need to do deconvolution of a given experimental M-point signal using the DFT, how do we avoid the circular effects. I think this is the gist of my long post. – AChem Jan 17 '21 at 23:05
zero-padding in the frequency domain will simply give you extra intermediate points in the time domain when you invert the Fourier transform; so it is again just a way to interpolate your data; you might as well interpolate in the time domain, so zero-padding in the frequency domain is not needed. – Carlo Beenakker Jan 18 '21 at 07:45
1

if you wish one more reference: "Zero padding is only suitable for convolution and not for deconvolution.", see Deconvolution of time series in the laboratory --- zero padding interpolates the transform, and if you are not interested or do not need an interpolated signal in the time domain, there is no need to zero-pad the signal in the frequency domain before you transform back to the time domain; does this answer your question? – Carlo Beenakker Jan 19 '21 at 11:47
Thanks, I had seen this paper. This is paper the which motivated this post. I agree zero-padding can be used for upsampling or interpolation but it can also be used for avoiding edge effects of the DFT, because you can discard edges and keep the deconvoluted signal intact. Now I am also seeing references now which strongly recommend doing zero padding. Could you have a look at Figure 1 and Figure 2 of "Deconvolution of periodic heat signals by fast fourier transform" https://www.sciencedirect.com/science/article/abs/pii/0040603187880206 – AChem Jan 19 '21 at 15:49
1

that paper only does zero-padding in the time domain, not in the frequency domain; edge effects appear when you convolute in the time domain, when you deconvolute by division in the frequency domain there are no edge effects, so there is no need to zero-pad in the frequency domain. – Carlo Beenakker Jan 19 '21 at 18:18
I think the question is boiling down to the point that if we have a N-point signal which needs to be deconvoluted by a M-point response function (M>N)? How much zero padding should we do in time domain to the N-point signal and consequently to the M-point response function in order to avoid wrap-around or circular effects of DFT. – AChem Jan 19 '21 at 23:14
1

this is answered in the first paragraph of section 4 of the IEEE paper : the signal $y$ has length $N_1\equiv N$ , the response function $h$ has length $N_2\equiv M\geq N$ and the time-domain padding should increase the length of both to $2N_1-1$ , assuming that $N_1 is a power of two. – Carlo Beenakker Jan 20 '21 at 10:46
What I am finding by trials if we have a full convolution ( call it a signal) of $y$ * $h$ ; it will have a length $N_1$ + $N_2$ -1 and if we need to do deconvolution, $h$ must be padded in the time domain, equal to the length of convolution. We fully/rather exactly recover the exact $y$ with additional zeros. However, if I take a portion of that convolution i.e, change its length, nothing seems to recover the original shape, even if $h$ is exactly known. – AChem Jan 20 '21 at 16:35

Deconvolution using the discrete Fourier transform

1 Answers1