TL;DR
Peter Taylor pointed out that the expressions below reduce to
$$\lim_{n\rightarrow k}x^{-n}I_n(x)= (x-1) \sum_{i=0}^k \frac{H_{k+1} - H_i}{x^{i+1}} -2 \,\text{arctanh}\,(1-2 x)$$
$\newcommand\HGF{_2\!\tilde{F}_1}$Mathematica is able to compute these limits, the result is in terms of a partial derivative of the regularized hypergeometric function $\HGF$. For $k=2$ I find
$$\lim_{k\rightarrow 2}x^{-k}I_k(x)=\frac{11}{3}-\gamma_{\text{Euler}}+\ln x-\frac{1}{6x^3}\left({\HGF^{(0,0,1,0)}}(-3,1,-2;x)+{\HGF^{(1,0,0,0)}}(-3,1,-2;x)\right).$$
The superscript notation is Mathematica's way of indicating which variable to differentiate. As a test, for $x=1/2$ the right-hand-side evaluates to $-4.833333\cdots=-29/6$, which agrees with a numerical evaluation of $\lim_{k\rightarrow 2}[\beta_x( -1 - k, 0) + H_{-2 - k}]$.
The corresponding formula for integer $k\geq 2$ is
$$\lim_{n\rightarrow k}x^{-n}I_n(x)=c_k-\gamma_{\text{Euler}}+\ln x-\frac{1}{(k+1)!x^{k+1}}\left({\HGF^{(0,0,1,0)}}(-k-1,1,-k;x)+ {\HGF^{(1,0,0,0)}}(-k-1,1,-k;x)\right).$$
The fraction $c_k$ is twice the constant term in an expansion of $H_{-2-n}$ around $n=k$.
I don't have a closed-form expression for $c_k$, the first few values are $11/3, 25/6, 137/30, 49/10, 363/70$, for $k=2,3,4,5,6$.
Update: As pointed out by Peter Taylor: $c_k=2H_{k+1}$.
Mathematica code.
k=6;
Series[Gamma[a]x^a Hypergeometric2F1Regularized[a,1-b,a+1,x],{a,-1-k,0}]/.b->0//Normal// FullSimplify;
%/.a->-1-x;
Series[HarmonicNumber[-2-x],{x,k,0}]//Normal;
%+%%//FullSimplify
The asympotics near $x=0$ and $x=1$ is
$$\lim_{n\rightarrow k}x^{-n}I_n(x)\rightarrow\begin{cases}
-\frac{1}{(k+1)x^{k+1}}&\text{for}\;\;x\rightarrow 0\\
-\ln(1-x)&\text{for}\;\;x\rightarrow 1
\end{cases}$$
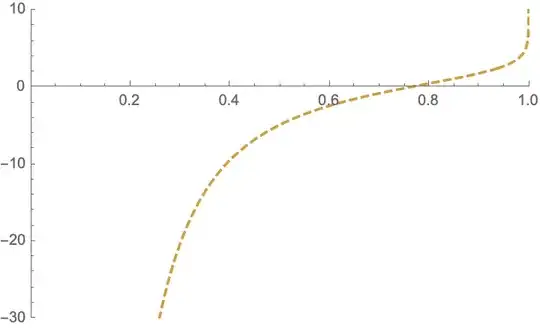
Here is a plot of $\lim_{n\rightarrow k}x^{-n}I_n(x)$ for $k=2$.
Special cases:
$$k=2:\quad\lim_{k\rightarrow 2}x^{-k}I_k(x)=\frac{(x-1) (11 x^2+5 x+2)}{6 x^3}-2 \,\text{arctanh}\,(1-2 x)$$
$$k=3:\quad\lim_{k\rightarrow 3}x^{-k}I_k(x)=\frac{(x-1) (25 x^3+13 x^2+7 x+3)}{12 x^4}-2 \,\text{arctanh}\,(1-2 x)$$
$$k=4:\quad\lim_{k\rightarrow 4}x^{-k}I_k(x)=\frac{(x-1) (12 + 27 x + 47 x^2 + 77 x^3 + 137 x^4)}{60 x^5}-2 \,\text{arctanh}\,(1-2 x)$$
$$k=5:\quad\lim_{k\rightarrow 5}x^{-k}I_k(x)=\frac{(x-1)(10 + 22 x + 37 x^2 + 57 x^3 + 87 x^4 + 147 x^5)}{60 x^6}-2 \,\text{arctanh}\,(1-2 x)$$
$$k=6:\quad\lim_{k\rightarrow 6}x^{-k}I_k(x)= \frac{(x-1) (1089 x^6+669 x^5+459 x^4+319 x^3+214 x^2+130 x+60)}{420 x^7}-2 \,\text{arctanh}\,(1-2 x)$$
$$k=\mathbf{10}:\quad\lim_{k\rightarrow 10}x^{-k}I_k(x)= \frac{(x-1) (83711 x^{10}+55991 x^9+42131 x^8+32891 x^7+25961 x^6+20417 x^5+15797 x^4+11837 x^3+8372 x^2+5292 x+2520)}{27720 x^{11}}-2 \,\text{arctanh}\,(1-2 x)$$
$$k=\mathbf{14}:\quad\lim_{k\rightarrow 14}x^{-k}I_k(x)= \frac{(x-1) (1195757 x^{14}+835397 x^{13}+655217 x^{12}+535097 x^{11}+445007 x^{10}+372935 x^9+312875 x^8+261395 x^7+216350 x^6+176310 x^5+140274 x^4+107514 x^3+77484 x^2+49764 x+24024)}{360360 x^{15}}-2 \,\text{arctanh}\,(1-2 x)$$
The pattern suggests this general form:
$$\lim_{n\rightarrow k}x^{-n}I_n(x)=\frac{x-1}{a_k x^{k+1}}\left(\sum_{p=0}^k b_{p,k} x^p\right) -2 \,\text{arctanh}\,(1-2 x)$$
with $a_k$ in OEIS:A003418 and $b_{p,k}$, $p=0,1,2\ldots k$, the rows of the triangle in OEIS:A027446.
