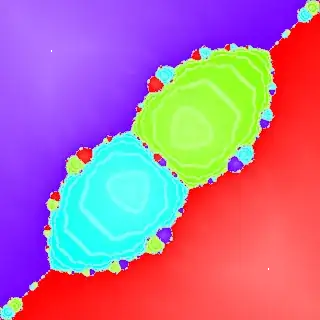
I've been tinkering with Newton's method applied to polynomials. E.g., Newton's method for $z^5 - 1 = 0$ gives:
There aren't a lot of symmetric patterns of finite sets of points in the plane, so I decided to rerun the code on the Riemann sphere using a version of Newton's method with spherical symmetry. I thought this would allow me to use point patterns corresponding to all the Platonic solids. However, only the tetrahedral case works:
This image has tetrahedral symmetry using the identification of $\mathbb{C}_\infty$ with $S^2$. However, in order to get a rational function with tetrahedral symmetry, we need to decide where to put the poles. A polynomial no longer works: all of its poles are at $\infty$, which is not symmetric. Happily, for a tetrahedron there is a convenient place to put the poles: in the middle of each face. The face centers are at the antipodes $-1/\bar{z}$ of the vertices, so our rational function is
$$f(z) = \prod_{k=1}^4 \frac{z-z_k}{z+1/\bar{z_k}}$$
where $z_{1\ldots4}$ are the stereographically projected vertices of the tetrahedron. This rational function has tetrahedral symmetry, so a spherically symmetric version of Newton's method applied to it produces a tetrahedrally symmetric image.
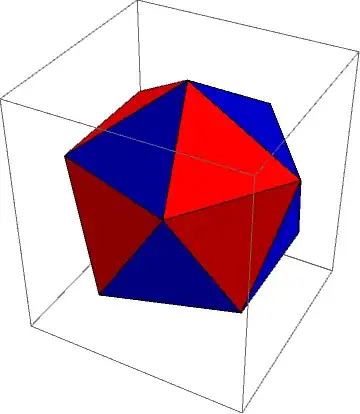
Unfortunately, all of the other Platonic solids have vertices at the antipodes of their vertices (they are symmetric under $p \mapsto -p$). Let's consider the icosahedron specifically:
Question: If we put a simple zero at each of the 12 vertices of the icosahedron, what's the most symmetric place to put 12 poles (not necessarily simple)?
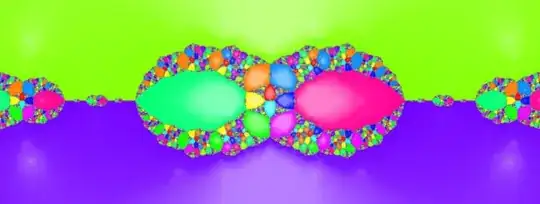
One answer is to inscribe a tetrahedron inside the icosahedron with tetrahedron vertices at face centers, and put order 3 poles at each tetrahedron vertex. This produces an image with tetrahedral symmetry:
Is that the best one can do?
Edit: Here's a version of the icosahedral symmetry one using @pregunton's linked rational function $F_{3,5}(z)$, but taking the fifth root to turn the zeros back into simple zeros and the order 3 poles into order $3/5$ singularities since that produces a slightly nicer picture:
Higher resolution versions of these images: quintic, tetrahedron, icosahedron, modified icosahedron.