4

Homotopy categories can be thought of (e.g. on p205-6 of Context) as having arrows built from equivalence classes of special zigzags of arrows in their underlying category. Following this answer and comments, I have checked a list of 139 named categories, and I think that they fall into one of five cases:

  • Finite categories used in diagram/shape work
  • Zigzag-connected categories, including those with initial/terminal/zero objects
  • Disconnected groupoids like $\mathbb{P}$, whose objects are sets and arrows are bijections
  • Quillen model categories and homotopy categories
  • The quirky disconnected category $\mathbf{Field}$, whose objects are fields and arrows are field maps

I don't think there's an underlying pattern here, but I'm curious: Is the typical category or groupoid connected? I would understand if the question were only sensible or tractable for (in)finite collections of arrows. By "typical" I mean that I'll upvote any counting formalism which allows us to imagine randomly-chosen elements of $\mathbf{Cat}$, by analogy with questions about typical graphs or other combinatorial structures; or also, any metatheory or philosophy that explains why we look under a particular "streetlight" for interesting categories to study.

Corbin
  • 424
  • 1
    This is not how category theory works. I don't believe it's how any other mathematical discipline works (with certain very special exceptions such as finite simple groups). – Paul Taylor Jul 27 '21 at 21:42
  • 3
    This is not a well-defined question until you define what you mean by "typical." – John Klein Jul 27 '21 at 21:50
  • 5
    This question seems directly analogous to questions like "is the typical graph connected?" In that case it's clear that this very much can be an interesting mathematical question (percolation theory), one just has to define the probability distribution one is using first, and the question carries no meaning without fixing something like that. – Will Sawin Jul 27 '21 at 22:04
  • 6
    The category of fields of any particular fixed characteristic is connected, though, and the category of fields decomposes as a disjoint union of those connected subcategories. When encountering a disconnected category, my first impulse is to ask how many connected component subcategories it has, and then to investigate each of the connected components individually. I imagine this is also a reflex many other mathematicians have. Perhaps this is why we may feel that "most" categories are connected: when they aren't, we are accustomed to immediately splitting them into their connected components. –  Jul 27 '21 at 22:06
  • 3
    @PaulTaylor I'm not really sure what aspect of the question you're objecting to. I think we can all agree, though, that a lot here hinges on what is meant by "typical". To start, we should distinguish between "typical" in the sense of "natural, commonly encountered" versus "typical" in some more objective sense, as illustrated nicely in this recent question. A.S. has addressed the former meaning of "typical" in the comment above and the latter meaning in the answer below. – Tim Campion Jul 28 '21 at 00:55
  • 2
    I've explained myself more; you all basically correctly guessed my mind. @PaulTaylor: I'm prototyping something akin to LMFDB for categories; that's why I've been asking these sorts of bizarre structural questions. – Corbin Aug 01 '21 at 15:21

1 Answers1

8

I apologize that this is not a full answer to your question, but rather an attempt to narrow its focus in a way that I hope is useful, and which at least leads to some interesting numerical data.

Preorders (i.e., quasiorders: sets equipped with a transitive, reflexive binary relation) are categories of the simplest kind, i.e., categories which have at most one morphism from any given object to any other given object. Perhaps it is reasonable to take, as a first approximation to your question, the question of how likely it is for a random preorder to be connected. To make the question precise: for each positive integer $n$, let $\bar{P}(n)$ be the number of isomorphism classes of preorders with $n$ elements, and let $\bar{C}(n)$ be the number of isomorphism classes of connected preorders with $n$ elements. What is the ratio $\bar{C}(n)/\bar{P}(n)$, and does the limit $\lim_{n\rightarrow\infty}\bar{C}(n)/\bar{P}(n)$ perhaps converge?

From the OEIS's website, here is a type-written letter from John Wright to Neil Sloane from 1972, containing calculations of $\bar{C}(n)$ and $\bar{P}(n)$ for $n=1, \dots ,7$: 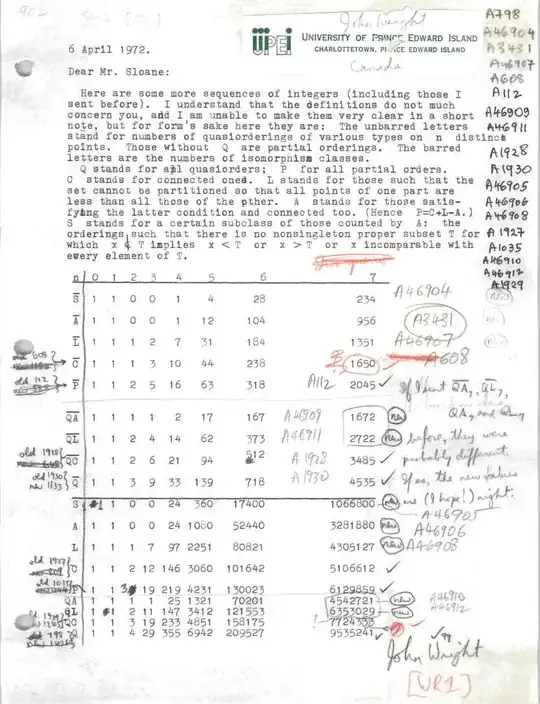enter image description here

I believe that the handwriting in the margins is Sloane's. I am writing $\bar{P}$ where Wright wrote $\bar{Q}$, because I think of $P$ standing for "preorders" (while Wright wrote $Q$ for quasiorders and $P$ for partial orders). Further calculations out to $n=16$ are found in the OEIS entries here http://oeis.org/A001930 , for $\bar{P}(n)$, and here http://oeis.org/A001928 , for $\bar{C}(n)$. (You will notice from the titles of these OEIS entries that they are about counting topologies, not preorders. It is a classical fact from combinatorics that every preordering on a set gives rise to a topology on that set, and for finite sets, in fact the topology carries the same data as the preordering. So in fact our question becomes: "what is the likelihood that a randomly-chosen homeomorphism class of finite topological spaces is connected?")

Here are some computed values of the ratio $\bar{C}(n)/\bar{P}(n)$, using the OEIS's tables:

  • $\bar{C}(1) = 1, \bar{P}(1) = 1$, with ratio $1$.
  • $\bar{C}(2) = 2, \bar{P}(2) = 3$, with ratio approx. $0.667$.
  • $\bar{C}(3) = 6, \bar{P}(3) = 9$, with ratio approx. $0.667$.
  • $\bar{C}(4) = 21, \bar{P}(4) = 33$, with ratio approx. $0.636$.
  • $\bar{C}(5) = 94, \bar{P}(5) = 139$, with ratio approx. $0.676$.
  • $\bar{C}(6) = 512, \bar{P}(6) = 718$, with ratio approx. $0.713$.
  • $\bar{C}(7) = 3485, \bar{P}(7) = 4535$, with ratio approx. $0.768$.
  • $\bar{C}(8) = 29515, \bar{P}(8) = 35979$, with ratio approx. $0.820$.
  • $\bar{C}(9) = 314474, \bar{P}(9) = 363083$, with ratio approx. $0.866$.
  • $\bar{C}(10) = 4255727, \bar{P}(10) = 4717687$, with ratio approx. $0.902$.
  • $\bar{C}(11) = 73831813, \bar{P}(11) = 79501654$, with ratio approx. $0.929$.
  • $\bar{C}(12) = 1653083021, \bar{P}(12) = 1744252509$, with ratio approx. $0.948$.
  • $\bar{C}(13) = 47941962135, \bar{P}(13) = 49872339897$, with ratio approx. $0.961$.
  • $\bar{C}(14) = 1803010446411, \bar{P}(14) = 1856792610995$, with ratio approx. $0.971$.
  • $\bar{C}(15) = 87882300251730, \bar{P}(15) = 89847422244493$, with ratio approx. $0.978$.
  • $\bar{C}(16) = 5543501326580737, \bar{P}(16) = 5637294117525695$, with ratio approx. $0.983$.

This numerical data gives a certain impression that "a randomly chosen isomorphism class of finite preorder is connected," but only an impression. To really know anything, one ought to show that $\lim_{n\rightarrow\infty}\bar{C}(n)/\bar{P}(n)$ converges to some positive number, and to get some bounds on that number. Perhaps the combinatorialists have already done this: I hope that people who know some combinatorics (which unfortunately does not include me) will weigh in on this.

I am sorry that this is at best only a very partial answer to the question. I would have left it as a comment if it weren't far too long.