Sampling uniformly in a ball of radius $\epsilon$ in the space of dicrete r.v. of m modalities for the total variation metric

Question

I am looking for some reference or an algorithm that allows to sample uniformly in the ball centered at a discrete random variable of n modalities in the TV distance.

For the record for 2 discrete random variables the total variation distance between them is defined by : $$d_{TV}(X,Y)= \sum _{i=1}^{n} |p_i-q_i|$$ where the laws of X and Y are defined by the vectors $(p_1,...,p_n)$ and $(q_1,...,q_n)$ with $ \sum _{i=1}^{n} p_i=1$ and $ \sum _{i=1}^{n} q_i=1$

This is not as simple as it may look but quite natural problem though but I couldn't find any reference for this problem.

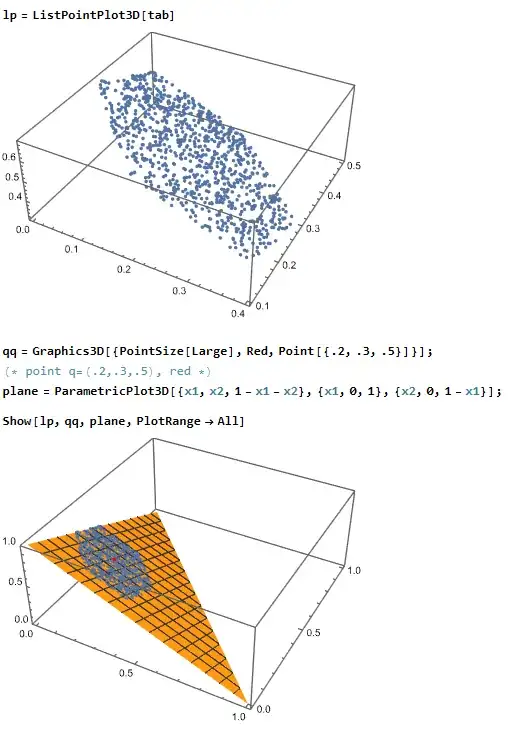
Edit : I will try to clarify the problem, the objective is to sample in the space of discrete random variables with $n$ modalities not sampling from those random variables. Any point in this space is thus characterized by the n dimensional vector of their law i.e. $p=(p_1,...,p_n)$ such that $ \sum _{i=1}^{n} p_i=1$. This space is endowed with the total variation distance defined above. For a fixed point $X$ or alternatively $p$ in this space I can define a ball with respect to this metric for some $0\leq\epsilon\leq 1$ (even though the case $\epsilon= 1$ is the whole space unless mistaken).

So once I have fixed $p$ and $\epsilon$ I am looking to sample uniformly in this ball, to get $\tilde{q}$. For the $\epsilon= 1$ case I think that a Dirichlet law with parameters $(1,...,1)$ might do the trick because unless mistaken it allows to sample uniformly over the $n-simplex$ but for the restricted case of a non trivial ball I am a bit confused and do not have a clue how to make a sampling algorithm that might just do the trick.

It is unclear what you want to sample: random variables (r.v.'s) with values in the set ${1,\dots,n}$? Do you want to specify the probability space(s) on which such r.v's are defined? How do you define the uniform distribution on the set of such r.v.'s? — Iosif Pinelis, Sep 19 '21 at 16:01
This is still unclear: "the objective is to sample in the space of discrete random variables". Why random variables (which are real-valued functions)? It seems you rather want to sample just from a neighborhood of a point of the simplex, right? — Iosif Pinelis, Sep 19 '21 at 18:48
Right, I identify those points to the laws of discrete r.v. with n modalities, this why I interpret this as sampling in the space of those r.v. endowed with the TV metric. — The Bridge, Sep 19 '21 at 18:55
Well typically n would be something like 4 or 5, some outlier cases might reach 30 at most though. — The Bridge, Sep 20 '21 at 07:04

Iosif Pinelis · Accepted Answer · 2021-09-20T00:59:03.683

2

For the uniform sampling from general convex polytopes, see e.g. Answer 1, Answer 2, other answers to this Question, and further references given there. Also, for instance, Fast MCMC Sampling Algorithms on Polytopes.

Here is an example with $1000$ sample points for $n=3$, $q=(.2, .3, .5)$, and $\epsilon=.4$, generated by a Markov Chain Monte Carlo method (with $5$ steps for each of the $1000$ sample points:

edited Sep 20 '21 at 00:59

answered Sep 19 '21 at 20:43

Iosif Pinelis

116,648

Thank you for this great answer which is very well illustrated. – The Bridge Sep 20 '21 at 13:06

Sampling uniformly in a ball of radius $\epsilon$ in the space of dicrete r.v. of m modalities for the total variation metric

1 Answers1