Does it make sense to express upper bounds on arithmetic sequences with Dirichlet generating functions?

Question

In order to see what happens when taking the functional equation in this form: $$\xi(s) := \pi^{-s/2}\ \Gamma\left(\frac{s}{2}\right)\ \zeta(s) $$ $$\xi(s) = \xi(1 - s)$$ $$\pi^{-s/2}\ \Gamma\left(\frac{s}{2}\right)\ \zeta(s)=\pi^{-(1-s)/2}\ \Gamma\left(\frac{1-s}{2}\right)\ \zeta(1-s)\tag{$\ast$}$$

and applying it to this Dirichlet generating function (in two variables):

$$\frac{\zeta(s)\ \zeta(c)}{\zeta(s+c-1)}\tag{$\ast \ast$}$$

associated with the GCD matrix that has the property stated more clearly by GH from MO here:

$$\Lambda(m)=\lim_{s\to 1+}\zeta(s)\sum_{d\mid m}\frac{\mu(d)}{d^{s-1}}=\lim_{s\to 1+}\;\sum_{n=1}^\infty\frac{1}{n^s}\left(\sum_{d\mid\gcd(n,m)}d\mu(d)\right),\qquad m>1.$$

Applying $(\ast)$ to $( \ast \ast )$ we get:

$$\frac{\pi^{-s/2}\ \pi^{-c/2}}{\pi^{-s/2-c/2+1/2}}\ \frac{\Gamma\left(\frac{s}{2}\right)\Gamma\left(\frac{c}{2}\right)}{\Gamma\left(\frac{s}{2}+\frac{c}{2}-\frac{1}{2}\right)}\ \frac{\zeta(s)\ \zeta(c)}{\zeta(s+c-1)}=\frac{\pi^{-(1-s)/2}\ \pi^{-(1-c)/2}}{\pi^{-((1-s)+(1-c)-(1-1))/2}}\ \frac{\Gamma\left(\frac{1-s}{2}\right)\ \Gamma\left(\frac{1-c}{2}\right)}{\Gamma\left(\frac{1-s}{2}+\frac{1-c}{2}-\frac{1-1}{2}\right)}\ \frac{\zeta(1-s)\ \zeta(1-c)}{\zeta((1-s)+(1-c)-(1-1))}$$

Moving the Riemann zeta functions to the left hand side, we get:

$$\frac{\zeta(s)\ \zeta(c)}{\zeta(s+c-1)}\ \frac{\zeta((1-s)+(1-c)-(1-1))}{\zeta(1-s)\ \zeta(1-c)}=\frac{\pi^{-(1-s)/2}\ \pi^{-(1-c)/2}}{\pi^{-((1-s)+(1-c)-(1-1))/2}}\frac{\pi^{-s/2-c/2+1/2}}{\pi^{-s/2}\ \pi^{-c/2}}\ \frac{\Gamma\left(\frac{1-s}{2}\right)\ \Gamma\left(\frac{1-c}{2}\right)}{\Gamma\left(\frac{1-s}{2}+\frac{1-c}{2}-\frac{1-1}{2}\right)}\ \frac{\Gamma\left(\frac{s}{2}+\frac{c}{2}-\frac{1}{2}\right)}{\Gamma\left(\frac{s}{2}\right)\Gamma\left(\frac{c}{2}\right)} \tag{$\ast \ast \ast$}$$

If replace the variable $s$ in: $$\frac{\zeta(s)\ \zeta(c)}{\zeta(s+c-1)}\ \frac{\zeta((1-s)+(1-c)-(1-1))}{\zeta(1-s)\ \zeta(1-c)}$$ with $s=\frac{1}{2}+it$, and let $c=1+\frac{1}{2}$, so that we get:

$$\frac{\zeta(\frac{1}{2}+it)\ \zeta(1+\frac{1}{2})}{\zeta(\frac{1}{2}+it+1+\frac{1}{2}-1)}\ \frac{\zeta((1-(\frac{1}{2}+it))+(1-(1+\frac{1}{2}))-(1-1))}{\zeta(1-(\frac{1}{2}+it))\ \zeta(1-(1+\frac{1}{2}))}$$

Plotting the negated real part:

$$-\frac{\zeta \left(\frac{3}{2}\right)}{\zeta \left(-\frac{1}{2}\right)}\Re\left(\frac{\zeta \left(\frac{1}{2}+i t\right) \zeta (-i t)}{\zeta \left(\frac{1}{2}-i t\right) \zeta (1+i t)}\right) \approx \sqrt{8 \pi t}$$

we observe that the function is close to $\sqrt{8 \pi t}$ as $t \rightarrow \infty$.

The constant: $-\frac{\zeta \left(\frac{3}{2}\right)}{\zeta \left(-\frac{1}{2}\right)}=$N[-Zeta[3/2]/Zeta[-1/2], 40]=12.56637061435917295385... has something to do with quasicrystals according the OEIS.

Mathematica:

Plot[-Re[(Zeta[3/2]*Zeta[1/2 + I*t]*Zeta[(-I)*t])/(Zeta[-(1/2)]*
  Zeta[1/2 - I*t]*Zeta[1 + I*t])], {t, 0, 60}]
Plot[Sqrt[8Pit], {t, 0, 60}]

Plot in Wolfram Alpha

The proof of this asymptotic should follow somehow from asymptotic properties of the Beta function in the functional equation, which we started with.

What I am more interested in is the overall approach. Is it worth expressing the Lowell Schoenfeld upper bound:

$|\psi(x)-x|\le\frac{\sqrt x\,\ln^2 x}{8\pi}$

in this way to make progress on the RH? Or is there some obvious drawback? The philosophy is similar to this question, where the goal was to use the expansion of the Chebyshev psi function in order to relate it to square roots.

Notice that the logarithm part is: $$\Re\left(\frac{\zeta '\left(\frac{1}{2}+i t\right)}{\zeta \left(i t+\frac{1}{2}\right)}\right)^2 \approx \left(\frac{1}{2} \log \left(\frac{t}{2 \pi }\right)\right)^2$$

by series expansion of the derivative of Riemann Siegel Theta function. And:

$$\lim_{c\to 1} \, \left(\frac{\zeta (c) \zeta (s)}{\zeta (c+s-1)}-\zeta (c)\right)=-\frac{\zeta '(s)}{\zeta (s)}$$

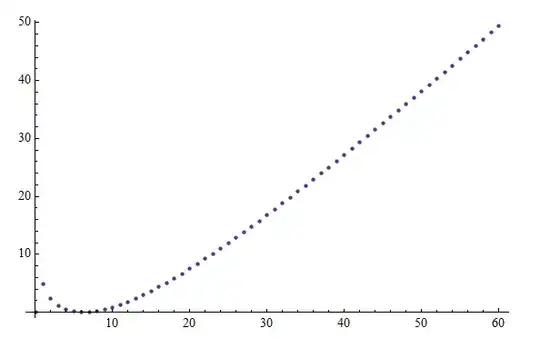
Plot of:

$$f(t)=-\frac{\zeta \left(\frac{3}{2}\right)}{\zeta \left(-\frac{1}{2}\right)}\Re\left(\frac{\zeta \left(\frac{1}{2}+i t\right) \zeta (-i t)}{\zeta \left(\frac{1}{2}-i t\right) \zeta (1+i t)}\right)\Re\left(\frac{\zeta '\left(\frac{1}{2}+i t\right)}{\zeta \left(i t+\frac{1}{2}\right)}\right)^2$$

Or which is the same:

$$f(t)=-\Re\left(\frac{\left(\zeta (c) \zeta \left(i t+\frac{1}{2}\right)\right) \zeta \left(-c-\left(i t+\frac{1}{2}\right)+2\right)}{\zeta \left(c+\left(i t+\frac{1}{2}\right)-1\right) \left(\zeta (1-c) \zeta \left(1-\left(i t+\frac{1}{2}\right)\right)\right)}\right) \Re\left(\frac{\zeta '\left(\frac{1}{2}+i t\right)}{\zeta \left(i t+\frac{1}{2}\right)}\right)^2$$

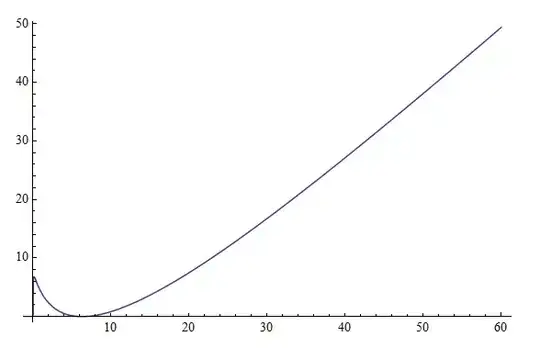
Plot of:

$$g(t)=\sqrt{8 \pi t} \left(\frac{1}{2} \log \left(\frac{t}{2 \pi }\right)\right)^2$$

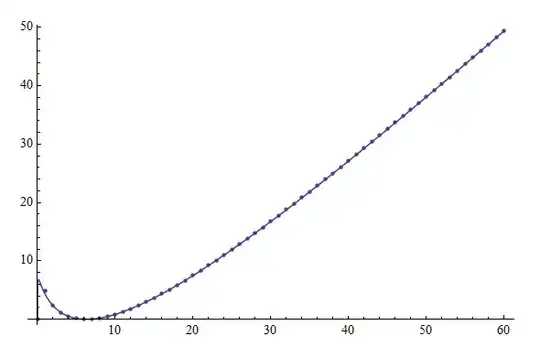
Curves $f(t)$ and $g(t)$ plotted together:

And the comparison of $g(t)$ with $\sqrt{t} \log ^2(t)$: $$\lim_{t\to \infty } \, \frac{\sqrt{8 \pi t} \left(\frac{1}{2} \log \left(\frac{t}{2 \pi }\right)\right)^2}{\sqrt{t} \log ^2(t)} = \sqrt{\frac{\pi }{2}}$$

Clear[s, c, t, r, q];
c = 1 + 1/2;
r = 1 + 1/1000;
ListPlot[Table[-Re[(Zeta[(1/2 + I*t)] Zeta[c] )/
      Zeta[-1 + c + (1/2 + I*t)]  * 
      Zeta[2 - c - (1/2 + I*t)]/(Zeta[1 - (1/2 + I*t)]*Zeta[1 - c])]*
   Re[Zeta'[(1/2 + I*t)] /Zeta[(1/2 + I*t)]  ]^2, {t, 0, 60, 1}], 
 DataRange -> {0, 60}]
Plot[Sqrt[8*Pi*t]*(1/2 Log[t/(2 \[Pi])])^2, {t, 0, 60}]
Show[%%, %]
ListLinePlot[
 Table[-Re[(Zeta[(1/2 + I*t)] Zeta[c] )/Zeta[-1 + c + (1/2 + I*t)]  * 
       Zeta[2 - c - (1/2 + I*t)]/(Zeta[1 - (1/2 + I*t)] Zeta[1 - c])]*
    Re[Zeta'[(1/2 + I*t)] /Zeta[(1/2 + I*t)]  ]^2 - 
   Sqrt[8*Pi*t]*(1/2 Log[t/(2 \[Pi])])^2, {t, 1/100, 60}]]
Clear[t];
Limit[(Sqrt[8*Pi*t]*(1/2 Log[t/(2 \[Pi])])^2)/(Sqrt[t]*Log[t]^2), 
 t -> Infinity]