There may not be a solution defined in $[0,\infty)$. Consider for each $a\in\mathbb{R}^+$ the curve $\gamma_a:[0,\frac{\pi a}{2})\to\mathbb{R}^2$ given by $\gamma_a(t)=(t,\text{tan}(\frac{t}{a})-ta)$, for $t\in[0,\frac{\pi a}{2})$. E.g., here are the curves $\gamma_a$ for $a=0.6,0.9,1.2,1.5$, in red, green, blue and orange respectively.
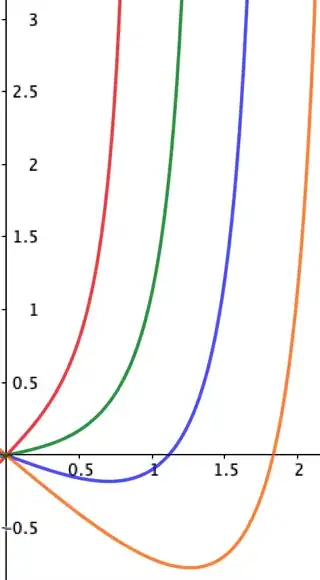
We will show that there is an initial value problem of the requested form for which the $\gamma_a$ are the only solutions, thus providing solutions on any $[0,b)$ but not on $[0,\infty)$.
The differential equation will use an appropriate inverse to the above function $\gamma$, so we begin by defining that inverse.
Each point $(t,x)\in(0,\infty)\times\mathbb{R}$ belongs to $\gamma_a$ for exactly one value of $a$, because such $a$ has to satisfy $t<\frac{\pi a}{2}$, so $a>\frac{2t}{\pi}$, and $x=\tan(\frac{t}{a})-ta$, and the function $a\mapsto\tan(\frac{t}{a})-ta$ decreases from $\infty$ to $-\infty$ when $a$ goes from $\frac{2t}{\pi}$ to $\infty$. Also, $a$ depends continuously on the point $(t,x)$.
In fact, $a$ depends smoothly on $(t,x)$: this is because, near a given point $(x_0,t_0)$, the values of $a$ are given by the function $\phi(x,t)$ such that, if $F(x,t,a)=x-\tan(\frac{t}{a})+ta$, then we have $F(x,t,\phi(x,t))=0$. And $\frac{\partial F}{\partial a}=t+\frac{t}{\cos^2(\frac{t}{a})a^2}\neq0$, so by the implicit function theorem $\phi$ is some $C^\infty$ function of $x,t$.
So if we arrange the function $f:(0,\infty)\times\mathbb{R}\to\mathbb{R}$ so that the solutions of the differential equation follow the curves $\gamma_a$, then none of these solutions are defined on $[0,\infty)$. Such a function $f$ can be expressed explicitly as $f(t,x(t))=-a-\frac{1}{\cos^2(\frac{t}{a})a}$, where $a=\phi(x,t)$. Indeed, this guarantees that for any fixed $a$, the curves $x(t)=\tan(\frac{t}{a})-ta$ are solutions of $x'(t)=f(x,t)$ for $t\in(0,\frac{\pi a}{2})$.
Moreover, those are all the solutions to the equation. This is because if a solution $x(t)$ passes through some point $(x_0,t_0)$ with $t_0>0$, then the curve $\gamma(t)=(t,x(t))$ satisfies the equation $\gamma'(t)=(1,f(x,t))$. So as the function $(x,t)\mapsto(1,f(x,t))$ is $C^\infty$, by the Picard Lindelöf theorem we have a unique solution $\gamma(t)=\gamma_a(t)$ for all $t\in(0,\frac{\pi a}{2})$, where $a=\phi(t_0,x_0)$.
