Desargues ten point configuration $D_{10}$ in LaTeX

Question

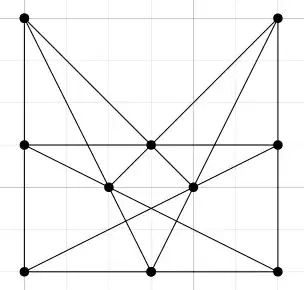
I want to draw the Desargues configuration $10_3$ in LaTeX using the standard picture environment, which allows only lines with the slopes $n:m$ where $\max\{|n|,|m|\}\le 6$. Is it possible? If not, then what is the smallest number $s$ for which there exists a drawing of the Desargues configuration $10_3$ in which all lines have slopes $n:m$ with $\max\{|n|,|m|\}\le s$? And for this smallest $s$, what is the smallest number $c$ for which there exists a drawing of the Desargues configuration $10_3$ in which all lines have slopes $n:m$ with $\max\{|n|,|m|\}\le s$ and all points have integer coordinates $(x,y)$ with $\max\{|x|,|y|\}\le c$?

Answer 1

This example shows that $s\le 2$ and for this $s$, $c\le 3$. Note that we are lucky with the latter, because there is a configuration for which every combinatorially equivalent realization has at least one irrational number as one of its coordinates.