11

Cross-posted from HSM: I posted this question a bit more than a week ago but have not gotten any answers at HSM. The only comment on the posting asks if I would accept polyhedral pictures illustrating the Euler characteristic -- the answer is "no".

EDIT 2023-08-15: Several commenters have asked me to sharpen the original question. I've now tried to do that.

Papers and books in geometry have been using illustrations for ages - for example there are figures in papyrus rolls containing bits of Euclid's Elements. My question, then, is

What are some of the earliest non-trivial illustrations of topological ideas appearing in published mathematical articles?

I am particularly interested in tracing the history of illustration in modern geometric (or "low-dimensional") topology. So I am mostly looking for early pictures of knots and surfaces (and three-manifolds - I give an example due to Poincaré below). But all examples are welcome!

Examples and non-examples:

  1. Non-example: The diagrams in editions of Euclid are always slightly wonky - drawing the Platonic ideal circle is impossible! So they are topological illustrations of geometric ideas.

  2. Example: The Heegaard diagram [Figure 4] in the fifth supplement to Analysis Situs [Poincaré, 1904]. It is not clear how Poincaré found this example and it is not clear how else he might have communicated the information.

  3. Non-examples: The various carved Celtic knots, or braids appearing as the frames of mosaics, or the coat of arms of the House of Borromeo, or metal links made of many unknots, or indeed textile arts (much older than publishing and, indeed, writing). Of course such artefacts are important, mathematical, and ancient. But it is impossible to point at one of them and say "this was the first one". This is why (perhaps wrongly!) I have restricted to "published" papers.

  4. Non-example: Euler's diagram [1735] of the bridges of Konigsberg does not count. This is because (I feel that) (a) it is a bit too close to a literal (as opposed to topological) figure and (b) graph theory is more properly a subfield of combinatorics, rather than of topology. (Of course, some people (such as Euler) disagree with (b).)

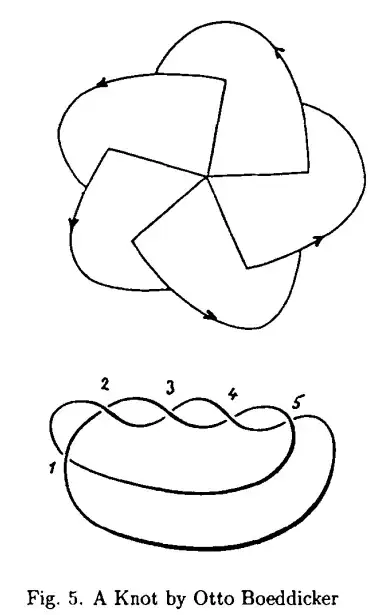
  5. Example: Listing's figures of knots [1848] in Vorstudien zur Topologie. The classic example, inspiring Tait's work on knot tabulation.

Sam Nead
  • 26,191
  • 9
    What do you mean with a "topological illustration"? – Wojowu Aug 14 '23 at 12:06
  • 2
    Related to the above comment: There are illustrations on Leibniz of adjoining points at infinity in perspective geometry (this was before projective geometry was officially born, even though pioneering work by Desargues already existed). Does that count as "topological"? – Mikhail Katz Aug 14 '23 at 12:07
  • 1
    @Wojowu - I think neither "topological" nor "illustration" can be given crystal clear definitions - this is why I gave examples! If forced, I would say that a "topological illustration" is one that "shows large-scale topological structure while making clear that the exact position is not so important". [And I suppose that it should be a topological illustration of something in topology... if somebody shows us a picture of a circle and says "this is a topological illustration of a round circle in the plane" then that is a bit silly?] – Sam Nead Aug 14 '23 at 12:11
  • @MikhailKatz - Interesting. I would guess not (??) but please give an answer and a link. I promise to look at it (and up-vote it, and encourage others to do the same, if they are so moved...) – Sam Nead Aug 14 '23 at 12:13
  • 1
    I don't see any basis for regarding graph theory as "not topological", even if it involves a lot of combinatorics. In any case, what about Euler's formula V-E+F = 2 for a polyhedron (that is topologically a 2-sphere)? Did he not include any diagram? – Daniel Asimov Aug 14 '23 at 13:41
  • 2
    @DanielAsimov, it seems to me that the spirit of the question is that something that's recognizably a polyhedron, i.e., a PL structure, falls a bit short of topology. On the other hand, an early figure illustrating the Euler characteristic for surfaces of positive genus would seem to fit the spirit of the question better. – Mikhail Katz Aug 14 '23 at 14:02
  • 3
    Mikhail Katz — you may be entirely right about the spirit of the question, which I am finding to be extremely vague. – Daniel Asimov Aug 14 '23 at 15:11
  • @DanielAsimov - please feel free to give an answer below - I'll certainly take a look. I was hoping that the several examples I gave would be helpful... to be honest, I was expecting some answer along the lines of "the first Mobius strip" or "the first Klein bottle" or "the first topological proof of the existence of a fixed point"... – Sam Nead Aug 14 '23 at 15:18
  • 3
    Not the oldest, but one of the simplest illustrations is in a book about convergence spaces (abstraction of topological spaces): Fig 1 "The empty convergence space", preceded by a few blank lines. (It was the only "illustration" in this book.) – Dominic van der Zypen Aug 14 '23 at 18:37
  • @Wojowu, MikhailKatz, DanielAsimov - I have edited the question to reflect/address your comments. Please, let me know if this is clearer. – Sam Nead Aug 15 '23 at 06:48
  • Thank you Sam. I acknowledge it is impossible to make this question precise, but I appreciate the effort to narrow down what it is that you look for. – Wojowu Aug 16 '23 at 14:59

4 Answers4

15

In view of Mikhail Katz' comment this is definitely not the oldest one, but there are drawings of knots in Gauss' mathematical diaries

enter image description here

enter image description here

UPD. Vandermonde, Remarques sur les problèmes de situation (1771):

enter image description here

Dmitrii Korshunov
  • 2,147
  • 4
    Is this genuine? I had no idea that Gauss wrote anything in English. – Daniel Asimov Aug 14 '23 at 16:09
  • What is this supposed to be an illustration of? I find the handwriting hard to read. – Mikhail Katz Aug 14 '23 at 16:35
  • 2
    @DanielAsimov that was a page from Maxwell's letter. Thanks for noticing. – Dmitrii Korshunov Aug 14 '23 at 17:32
  • 1
    Very nice! Certainly the braid group is very topological.... but does this count as "published"? Also, is there a link? – Sam Nead Aug 14 '23 at 17:32
  • @Sam, Since this is page 283 of "Handbuch 7", it appears that a book exists :-) MK – Mikhail Katz Aug 14 '23 at 17:38
  • 1

    Also, is there a link?

    unfortunately i couldn't find Handbuchs on the internet. i took the first picture form a survey of Przytycki (arXiv:math/0703096 ), apparently he scanned it himself from a manuscript in an "Old library in Gottingen" and the second one from "Orbits of Asteroids, a Braid, and the First Link Invariant" by Moritz Epple

     – Dmitrii Korshunov Aug 14 '23 at 18:49
  • 6
    @DanielAsimov

    I had no idea that Gauss wrote anything in English.

    He actually did.

    “One of the oldest notes by Gauss to be found among his papers is a sheet of paper with the date 1794. It bears the heading “A collection of knots” and contains thirteen neatly sketched views of knots with English names written beside them... With it are two additional pieces of paper with sketches of knots. One is dated 1819; the other is much later, ...”

     – Dmitrii Korshunov Aug 14 '23 at 18:51
  • 7
    yes, Gauss wrote about knots in English: for the original notebook drawings, see https://mathoverflow.net/a/383248/11260 – Carlo Beenakker Aug 14 '23 at 20:03
  • 5
    "...is there a link?" Is that a pun? – Gerry Myerson Aug 15 '23 at 03:45
10

Leibniz provides an illustration of adjoining a point at infinity in perspective geometry in a 1683 text entitled Elementa nova matheseos universalis. It can be found in the Akademie edition, A.VI. 4A. 521. The editors are not mathematicians so the figure seems rather botched, but the point $B$ is recognizably the (projective) point at infinity. The article was cited in our text in Review of Symbolic Logic. It would be interesting to find the original text to see what the picture looked like.

Mikhail Katz
  • 15,081
  • 1
  • 50
  • 119
  • 1
    I think that you are referring to the figure on page 13 of the following PDF file: https://www.uni-muenster.de/Leibniz/DatenVI4/VI4a2.pdf – Sam Nead Aug 15 '23 at 06:34
  • 1
    I think that this is indisputably a (very nice, very early!) topological picture of a fundamental construction in projective geometry. I'll clarify my question. – Sam Nead Aug 15 '23 at 06:35
  • @SamNead, I happen to have a pdf for Desargues' Brouillon Project which would provide an even earlier occurrence... if it contained any figures :-) I don't happen to have any pdfs by Kepler; it may be worth checking whether his work on conic sections contains illustrations. By the way, he referred to an ideal point at infinity as a "blind focus" (of what we would call a pencil of parallel lines). – Mikhail Katz Aug 15 '23 at 15:45
3

In the 1996 book History and Science of Knots, one of the essays is specifically on early knot history and in addition to what's already been mentioned here, they also include an illustration of a knot by the German astronomer (?) Otto Boeddicker from one of his papers. He published work analysing Gauss's integral for counting linking numbers in knots and also on the connection between knots and Riemannian surfaces, so this is definitely situated in a topological context.

diagram of a knot

The essay includes a bit more context in addition to references to Otto's original work. Source to it can be found here.

Nobilis
  • 323
  • 1
    Otto Boeddicker (1853–1937) – Mikhail Katz Aug 16 '23 at 14:38
  • 2
    I actually wonder if it's that same Otto Boeddicker that is listed online as an astronomer and lived in this time period. I couldn't find much in German about him, and in English there are only mentions of his work as an astronomer. The book in question is the only place I know of that discusses his work on knot theory. The Maths Genealogy Project lists his PhD dissertation cited in the essay I mentioned so for sure there is an Otto Boeddicker who worked on knots. – Nobilis Aug 16 '23 at 15:20
  • 2
    This source at Michigan gives the same birth year and cites his work on Gauss. – Mikhail Katz Aug 16 '23 at 15:31
  • @MikhailKatz Ah, amazing, thanks for sharing, it's got to be him then. – Nobilis Aug 16 '23 at 17:22
1

See page 9 and 10 of Riemann’s 1857 paper on abelian functions (where he introduced Riemann surfaces): https://www.maths.tcd.ie/pub/HistMath/People/Riemann/AbelFn/AbelFn.pdf

I believe the illustrations represent multiply connected surfaces obtained via gluing planar regions along branch cuts.

Vik78
  • 487