Fundamental Examples

Question

It is not unusual that a single example or a very few shape an entire mathematical discipline. Can you give examples for such examples? (One example, or few, per post, please)

I'd love to learn about further basic or central examples and I think such examples serve as good invitations to various areas. (Which is why a bounty was offered.)

---

Related MO questions: What-are-your-favorite-instructional-counterexamples, Cannonical examples of algebraic structures, Counterexamples-in-algebra, individual-mathematical-objects-whose-study-amounts-to-a-subdiscipline, most-intricate-and-most-beautiful-structures-in-mathematics, counterexamples-in-algebraic-topology, algebraic-geometry-examples, what-could-be-some-potentially-useful-mathematical-databases, what-is-your-favorite-strange-function; Examples of eventual counterexamples ;

---

To make this question and the various examples a more useful source there is a designated answer to point out connections between the various examples we collected.

---

In order to make it a more useful source, I list all the answers in categories, and added (for most) a date and (for 2/5) a link to the answer which often offers more details. (~year means approximate year, *year means a year when an older example becomes central in view of some discovery, year? means that I am not sure if this is the correct year and ? means that I do not know the date. Please edit and correct.) Of course, if you see some important example missing, add it!

Logic and foundations: $\aleph_\omega$ (~1890), Russell's paradox (1901), Halting problem (1936), Goedel constructible universe L (1938), McKinsey formula in modal logic (~1941), 3SAT (*1970), The theory of Algebraically closed fields (ACF) (?),

Physics: Brachistochrone problem (1696), Ising model (1925), The harmonic oscillator,(?) Dirac's delta function (1927), Heisenberg model of 1-D chain of spin 1/2 atoms, (~1928), Feynman path integral (1948),

Real and Complex Analysis: Harmonic series (14th Cen.) {and Riemann zeta function (1859)}, the Gamma function (1720), li(x), The elliptic integral that launched Riemann surfaces (*1854?), Chebyshev polynomials (?1854) punctured open set in C^n (Hartog's theorem *1906 ?)

Partial differential equations: Laplace equation (1773), the heat equation, wave equation, Navier-Stokes equation (1822),KdV equations (1877),

Functional analysis: Unilateral shift, The spaces $\ell_p$, $L_p$ and $C(k)$, Tsirelson spaces (1974), Cuntz algebra,

Algebra: Polynomials (ancient?), Z (ancient?) and Z/6Z (Middle Ages?), symmetric and alternating groups (*1832), Gaussian integers ($Z[\sqrt -1]$) (1832), $Z[\sqrt(-5)]$,$su_3$ ($su_2)$, full matrix ring over a ring, $\operatorname{SL}_2(\mathbb{Z})$ and SU(2), quaternions (1843), p-adic numbers (1897), Young tableaux (1900) and Schur polynomials, cyclotomic fields, Hopf algebras (1941) Fischer-Griess monster (1973), Heisenberg group, ADE-classification (and Dynkin diagrams), Prufer p-groups,

Number Theory: conics and pythagorean triples (ancient), Fermat equation (1637), Riemann zeta function (1859) elliptic curves, transcendental numbers, Fermat hypersurfaces,

Probability: Normal distribution (1733), Brownian motion (1827), The percolation model (1957), The Gaussian Orthogonal Ensemble, the Gaussian Unitary Ensemble, and the Gaussian Symplectic Ensemble, SLE (1999),

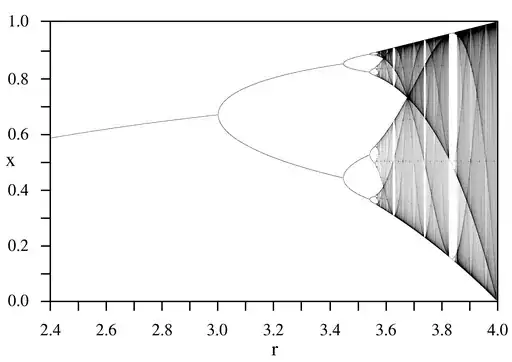
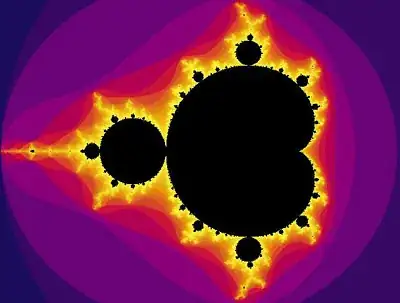
Dynamics: Logistic map (1845?), Smale's horseshoe map(1960). Mandelbrot set (1978/80) (Julia set), cat map, (Anosov diffeomorphism)

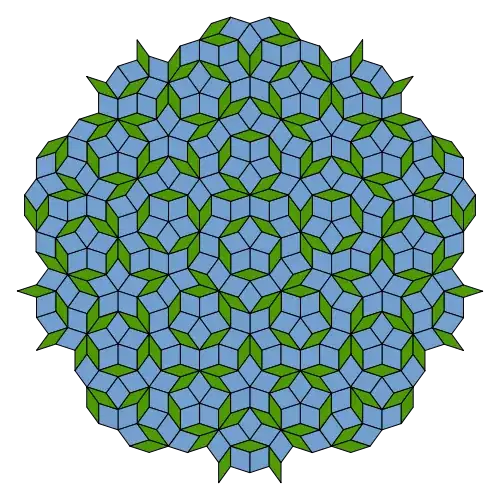
Geometry: Platonic solids (ancient), the Euclidean ball (ancient), The configuration of 27 lines on a cubic surface, The configurations of Desargues and Pappus, construction of regular heptadecagon (*1796), Hyperbolic geometry (1830), Reuleaux triangle (19th century), Fano plane (early 20th century ??), cyclic polytopes (1902), Delaunay triangulation (1934) Leech lattice (1965), Penrose tiling (1974), noncommutative torus, cone of positive semidefinite matrices, the associahedron (1961)

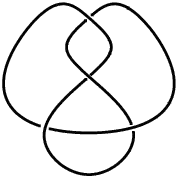
Topology: Spheres, Figure-eight knot (ancient), trefoil knot (ancient?) (Borromean rings (ancient?)), the torus (ancient?), Mobius strip (1858), Cantor set (1883), Projective spaces (complex, real, quanterionic..), Poincare dodecahedral sphere (1904), Homotopy group of spheres, Alexander polynomial (1923), Hopf fibration (1931), The standard embedding of the torus in R^3 (*1934 in Morse theory), pseudo-arcs (1948), Discrete metric spaces, Sorgenfrey line, Complex projective space, the cotangent bundle (?), The Grassmannian variety,homotopy group of spheres (*1951), Milnor exotic spheres (1965)

Graph theory: The seven bridges of Koenigsberg (1735), Petersen Graph (1886), two edge-colorings of K_6 (Ramsey's theorem 1930), K_33 and K_5 (Kuratowski's theorem 1930), Tutte graph (1946), Margulis's expanders (1973) and Ramanujan graphs (1986),

Combinatorics: tic-tac-toe (ancient Egypt(?)) (The game of nim (ancient China(?))), Pascal's triangle (China and Europe 17th), Catalan numbers (18th century), (Fibonacci sequence (12th century; probably ancient), Kirkman's schoolgirl problem (1850), surreal numbers (1969), alternating sign matrices (1982)

Algorithms and Computer Science: Newton Raphson method (17th century), Turing machine (1937), RSA (1977), universal quantum computer (1985)

Social Science: Prisoner's dilemma (1950) (and also the chicken game, chain store game, and centipede game), the model of exchange economy, second price auction (1961)

Statistics: the Lady Tasting Tea (?1920), Agricultural Field Experiments (Randomized Block Design, Analysis of Variance) (?1920), Neyman-Pearson lemma (?1930), Decision Theory (?1940), the Likelihood Function (?1920), Bootstrapping (?1975)

Answer 1

The integral $\int \frac{dx}{\sqrt{x(x-1)(x-\lambda)}}$ for $\lambda\neq 0,1$ essentially launched both complex analysis and algebraic geometry, via Riemann's discovery of the Riemann surface that is the natural domain of a function, leading to both analytic theory of Riemann surfaces and to the study of algebraic curves, leading to...complex analysis including in several variables and complex algebraic geometry, as we now know it.

Answer 2

Relevant to many areas (but mostly topology) is the Cantor set. It is an example of a set with properties too numerous to list here. To name a few: it is uncountable, compact, nowhere dense and it has Lebesgue measure 0.

Answer 3

The harmonic oscillator is a fundamental example in both classical and quantum mechanics.

Answer 4

The Petersen Graph in graph theory.

Answer 5

For a picture that launched a thousand papers, I'd nominate the bifurcation diagram of the logistic map.

(image via Wikipedia).

Answered by Martin M. W.

Answer 6

The Hopf fibration

Answer 7

The Fermat Equation xⁿ + yⁿ - zⁿ = 0.

This has truly been much more than an example in both algebra and number theory: it was one of the main motivations to develop the theory of unique factorization domains, Dedekind domains, class numbers, regular primes, etc. in the 19th century. In the late 20th century it provided a motivation for Wiles to work on modularity of elliptic curves.

In the 21st century, the equation c₁ x^a + c₂ y^b - c₃ z^c = 0 is similarly motivational for things like Q-curves, Galois representations, hypergeometric abelian varieties...

Answer 8

Brownian motion has a central role in the theory of stochastic processes

Answer 9

The Prisoner's Dilemma in Game Theory.

Answer 10

The Brachistochrone problem. Solved by both Newton/Bernoulli. It is considered to be the fundamental/first problem which led to the formulation of the Calculus of Variations.

Find the shape of the curve down which a bead sliding from rest and accelerated by gravity will slip (without friction) from one point to another in the least time.

Answer 11

In complex dynamics: The Mandelbrot set

Answer 12

There's always the venerable normal distribution (for probability theory).

Answer 13

Laplace's equation is the fundamental example of a PDE.

If I could broaden the question to allow a triumvirate of examples, I'd say Laplace's equation, the heat equation, and the wave equation are the canonical examples of PDEs, representing elliptic, parabolic, and hyperbolic equations respectively.

Answer 14

Someone has already mentioned tori, but I think elliptic curves in algebraic geometry merit their own separate mention.

Answered by Kevin Lin

Answer 15

Russell's paradox

Showing that Frege's set theory leads to contradiction.

The example can be described as the set of all sets $A$ such that $A \notin A$. It is related in spirit to Cantor's proof that a power set has larger cardinality than a set and to the ancient "liar paradox".

Answer 16

The cotangent bundle is the fundamental example of symplectic manifold/phase space.

Answer 17

Answered by James: The Platonic solids. They are fundamental, collectively and individually, to many areas of mathematics.

Answer 18

1The Fano plane in finite geometry

http://en.wikipedia.org/wiki/Fano_plane

Answer 19

SAT (Boolean satisfiability problem) in complexity theory/theoretical computer science -- it's the canonical example of an NP-complete problem not just because it came first, but because it launched a thousand other research papers all on its own. (3SAT is maybe more canonical, but the more general form is better to generalize and study for its own sake.)

Answered by: Harrison Brown

Answer 20

The Penrose tiling (image from Wikipedia). It's a fundamental example not just for aperiodic tilings more generally, but for Connes' work on noncommutative geometry.

Answer 21

The ring $\mathbb{Z}[\sqrt{-5}]$ is a fundamental example of non-unique factorization in rings in algebraic integers. Perhaps of more historical relevance is the example of $p=37$ that shows that Lamé's "proof" of Fermat's Last Theorem fails. I'm not sure Kummer used $p=37$ though. In any case, examples of non-unique factorization in rings in algebraic integers lead to the whole theory of ideal numbers and later Dedekind domains and set the tone for algebraic number theory.

Answer 22

The Catalan numbers are definitely a fundamental example in combinatorics.

Answered by Qiaochu Yuan

Answer 23

A lot of algebraic topology was developed with computing the higher homotopy groups of spheres in mind.

Answered by: David Lehavi

Answer 24

The quaternions

Probably the natural numbers, real numbers, and complex numbers are "too fundamental" to count here. But the field of quaternions discovered in the mid 19 century qualifies.

Answer 25

In geometry, group theory and other areas: The Leech Lattice:

Answer 26

The KdV equation in integrable systems. It was through a numerical study of KdV that the word soliton was coined. This numerical study lead to much analytical work, including the development of Lax Pairs. (Answer by Aaron Hoffman)

Answer 27

$$2^{\aleph_0} = \aleph_1$$

The Continuum Hypothesis is an example of an undecidable statement par excellence. It is an example of a problem that is:

• natural;
• historied -- it was first asked by Cantor himself;
• celebrated -- it was Hilbert's first of his famous 23 problems; and
• undecidable in a very deep way -- it's independent of all current large cardinal axioms, and in fact something deeper than this can be said, but that is currently beyond my understanding.

Moreover, the desire to "solve" CH was the main motivation, or at least one of the main motivations, for:

• Godel's description of the Constructible Universe, which has already been listed as a fundamental example in logic and foundations, and the beginnings of inner model theory; and
• Cohen's invention of the method of forcing which is now indispensable and ubiquitous in modern set theory, and also won Cohen a Fields medal.

Answer 28

It has often been said that if you understand $su_3$ you understand all simple Lie algebras, so that should make it the fundamental example. (Personally I think that it suffices to understand $su_2$!)

Answer 29

I do think Milnor's exotic sphere distinguish differential topology from general topology, but i don't know if this is an example of the kind you want.

Answered by: Yuhao Huang

Answer 30

The Noncommutative Torus in non-commutative geometry. (Maybe it has just shaped the subject because it is about the only thing one can handle explicitly)

Answer 31

Answered by Agol: The figure eight knot (complement) is the starting point for much of hyperbolic geometry. Although other hyperbolic manifolds were discovered before it, the figure eight knot complement has one of the simplest hyperbolic structures to analyze. Thurston first proved his hyperbolic Dehn surgery theorem for the figure eight knot complement - after understanding the proof in this case, the general case is not much harder to understand. It is the simplest knot for which every 3-manifold is a branched cover over it. It was one of the first (non-torus) knots for which the knot-complement problem was proven. It has the most number of non-hyperbolic Dehn-fillings over any one-cusped hyperbolic 3-manifold. It is the smallest volume orientable hyperbolic manifold with one cusp. It was the first knot proven that all non-trivial Dehn fillings have a finite-sheeted cover with positive first betti number. It was the first knot for which the volume conjecture has been verified.

(see also this Wikipedia article.)

^(source)

Answer 32

The Harmonic series 1+1/2+1/3+1/4+1/5+... and for that matter the Riemann zeta function.

Answer 33

Recursion theory has the halting problem. From it, you obtain the first example of an interesting Turing degree, and generalizing it, you get the Turing jump operator.

The halting problem also plays an important role in (the boundary of) computational complexity theory, since it's one of the main tools for demonstrating the insolubility of computational problems.

Answer 34

The p-adic numbers. Discovered only in 1897.

Answer 35

Dirac's Delta function

It was introduced by 1927 by Paul Dirac. Can be regarded as an important example towards the theory of distribution.

For examples of distributions to keep in mind see this question.

Answer 36

In the theory of holomorphic functions of several variables, Hartogs's theorem that any holomorphic function on a punctured open set of $\mathbb C^n$ ($n\geqslant 2$) can holomorphically be continued through the deleted point really started the subject and is still the most spectacular divide between $n \geqslant 2$ and $n=1$ [where it is completely false: on $\mathbb C^\ast$ look at 1/z or, worse, exp(1/z): these functions clearly can't be continued holomorphically through zero]

Answer 37

Smale's horseshoe map in dynamical systems.

Answer 38

$\operatorname{SL}_2(\mathbb{Z})$ and its action on the hyperbolic plane. It is the "minimal" example of mapping class groups and arithmetic groups. And one can already see a lot of the general behavior.

Answer 39

In combinatorics, the (Pascal) Binomial Triangle more or less started the entwining of combinatorics, probability and algebra.

The other two most seminal and ubiquituous triangles of numbers are the Stirling (duals between 1st and 2nd sort, permutation world and set world, the most often generalized family of numbers) and the Eulerian numbers (permutations seen as words on ordered alphabet), the reference statistics on permutations.

For links between combinatorics and number theory, I think the first prize would be the Bernoulli numbers.

Answer 40

The full matrix rings of any order over another ring (and their direct union of row-finite, column-finite matrices) are a fundamental example for Noncommutative Ring Theory: they are simple enough to be easily understood "in a glimpse" but complex enough to highlight many interesting concepts of the theory.

Answer 41

sl₂ is the fundamental example of a finite dimensional simple Lie algebra. It forms the basis of the Cartan-Killing classification of complex semisimple Lie algebras, since all of the others can be made by gluing (in some sense) copies of sl₂ together. Its representation theory is both straightforward and illuminating, since it points the way to the general theory of highest-weight representations.

For the same reason, SU(2) is the fundamental example of a nonabelian compact Lie group. By Borel-Weil, its irreducible representations can be geometrically realized as the spaces of sections of complex line bundles on the 2-sphere (somewhat easier to handle than a general flag variety).

Answer 42

The associahedron or Stasheff polytope.

_{(source: wikimedia.org)}

Answer 43

Various families of orthogonal polynomials can probably be considered fundamental in some way, but here I want to single out the Chebyshev polynomials, which seem to be the most miraculous. They have explicit formulas (T_n(x) = cos(n arccos(x)), for example), and they are closed under composition. Also, the polynomial of a given degree that has given bounds on an interval and grows as fast as possible outside the interval is a translated and scaled Chebyshev polynomial. The Chebyshev polynomials are fundamental in numerical analysis. Among their uses:

• Accurate numerical integration
• Accurate polynomial interpolation (if one is allowed to choose the evaluation points)
• Sometimes the mere existence of polynomials with the boundedness/growth properties of Chebyshev polynomials is useful, e. g., in analyzing the convergence of the method of conjugate gradients

(A little bit more on the relation to conjugate gradients: n steps of CG can be interpreted as optimizing something over the space of polynomials of degree n. The optimality of the Chebyshev polynomials in the sense of being as small as possible on [-1, 1] (stated above in a different form) is not quite equivalent to what CG requires, but it's close enough to imply that the optimal polynomial in the sense of CG must be very good (because it is at least as good as the Chebyshev polynomial).)

Answer 44

In operator theory, the unilateral shift. This operator is not only the fundamental example of an isometry on a Hilbert space, it can also be shown that this operator contains all other operators, in some sense.

Answer 45

Hyperbolic geometry, which led to the understanding that there are non Euclidean geometries and to many other developments.

Answer 46

Gödel's Constructible Universe, L, is the fundamental example of inner model theory. L was the first inner model, and is the minimal one. One could argue that the point of inner model theory is to build L-like models that do things L cannot.

Answer 47

Some people may disagree that this is an example per se, but I'd put up the Feynman path integral (see Wikipedia), because:

• it provided a completely new physical picture of quantum mechanics

• it led to systematic development of quantum field theory and string theories, both of which have had led to enormous synergistic growth in mathematics

• it uncovered a fundamental similarity between of stochastic processes and deterministic quantum dynamics

• it used the connection between Lie algebras and Lie groups in new and unexpected ways

• questions about the path measure have stimulated much development in measure theory and analysis

• tricks like the Wick rotation not only relate statistical mechanics and quantum mechanics (and the corresponding field theories) to each other, but also have stimulated further research in applications of analytic continuation

...and probably more that I am unaware of.

Answer 48

The torus is THE example in many branches of math. Algebraic Topology: it is the example where you can compute explicitly its fundamental group as well as its covering spaces, universal cover and everything else. Algebraic geometry: provided it is smooth, is a cubic which is not rational. It is a compact Lie group (and then a non so trivial example of a trivial tangent bundle). It is compact in $\mathbb{R}^4$ and has zero curvature (Riemannian geometry). It is a Riemann Surface. Actually one can compute very explicitly the moduli space of such Riemann surfaces as well as (very explicitly) the mapping class group (which is a beautiful example). It is an elliptic curve, an abelian variety... and it has all those properties I don't know about...meaning, an endless amount of properties.

Answer 49

The Heisenberg group: the group of 3 by 3 upper triangular matrices of the form

$$\begin{pmatrix} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 & 1 \end{pmatrix}.$$

When making a first step to non-commutativity? Or beyond planar models? Try the Heisenberg group.

Answer 50

Tsirelson space (see the Wiki entry for quick facts) in Banach space theory was seminal, in that it generated a stream of further refined and specialized counterexamples (most notably in the work of Casazza, Odell, Schlumprecht, and culminating in the famous examples of hereditarily indecomposable spaces by Gowers and Maurey (apologies for the countless others not mentioned here, but the list would be too long). Several long-standing conjectures (even dating back to Banach) have been proved or disproved using these examples, and the flow is not over even now.

Answer 51

The trefoil knot in knot theory.

Answer 52

In geometric/combinatorial group theory, Grigorchuk's 2-group is a fundamental example. It originally was constructed as a particularly elegant infinite finitely generated torsion group. Then Grigorchuk showed it had intermediate growth, answering Milnor's problem. For a time it was seen as the universal counterexample in group theory. But now it has spawned a theory of groups acting on rooted trees, self-similar groups and branch groups. Pierre de la Harpe has an entire chapter of his book devoted to this group.

Answer 53

Fundamental examples of coalgebraic structures:

• Homology-of-a-space Hopf algebra
• Hopf algebra representing a linear algebraic group
• Group rings
• Spheres as cogroups in the homotopy category of spaces

Answer 54

I think the seven bridges of Königsberg initiated a lot of modern discrete mathematics.

Answered by Tomaž Pisanski

Answer 55

The rational parametrization of the locus of the equation $X^2+Y^2=1$ by $(\frac{t^2-1}{t^2+1},\frac{2t}{t^2+1})$. It can be viewed geometrically by taking a line that intersects the unit circle at one rational point and then considering all possible (rational) slopes of the line (including infinity), which are in correspondence with (rational) points of the circle. This is the most basic example of using a geometric idea to find solutions to a diophantine equation, and it leads to very deep mathematics.

Answer 56

the Fischer-Griess Monster.

see:

http://en.wikipedia.org/wiki/Monster_group

Answer 57

Theory of Algebraically Closed Fields (ACF for short) is an important example in Model Theory. This was a motivation example to develop theory of stable and simple theories (leading, eventually, to a beautiful proof of Mordell-Lang conjecture by Ehud Hrushovski).

Answer 58

The Navier-Stokes equations.

Answered by Kristal Cantwell

Answer 59

The irrational rotation on the torus $\mathbb{T^2}$: $T_t (z,w) = (e^{2 \pi i \alpha }z, e^{2 \pi i \beta} w)$, where $\alpha, \beta \in \mathbb{R}, \frac{\alpha}{\beta} \notin \mathbb{Q}$. It is perhaps the first nontrivial example of an ergodic dynamical system. By considering its orbits $t \mapsto T_t (z,w)$, one gets examples of one-to-one immersions (with dense image) which are not embeddings, immersed submanifolds which are not closed/regular submanifolds, Lie subgroups which are not closed subgroups, non-Hausdorff quotient space and similar phenomena.

Answer 60

The ring of Gaussian integers Z[i] is a fundamental example of a ring of integers extending Z. Many early results in number theory were motivated by understanding and generalizing properties exhibited by Z[i] and its relationship with Z.

Answer 61

The Riemann zeta function is the fundamental example of a Dirichlet L-series. It is central in analytic number theory.

Answer 62

The Sorgenfrey line is an example that has motivated a lot of research in general topology, mostly generalized metric properties and ordered space theory. It's an example of a hereditary normal space with non-normal square, it is separable, Lindelöf, first countable, but not second countable; a generalized ordered space that is not orderable, and many more.

Answer 63

The complex projective space is the fundamental example in toric geometry, symplectic and GIT quotients,...

Answer 64

In convex geometry, the Euclidean ball. In fact (as I think Gil knows but many other readers here probably don't) a huge portion of (high-dimensional) convex geometry consists of results that show that arbitrary high-dimensional convex bodies behave like the Euclidean ball in various ways.

And if I may be permitted to add another complementary example or two, the simplex and cube are for many purposes the least "Euclidean ball-like" convex bodies, so they are useful for understanding the limitations of the Euclidean ball as a prototype for arbitrary bodies.

Answer 65

The cyclic polytope in the study of convex polytopes in high dimensions.

It is the convex hull of n points on the moment curve (t,t^2,t^3,...,t^d). It is simplicial and has the property that every [d/2] points form a face. (So, for example, in 4 dimension every two vertices form an edge.)

Answer 66

In modal logic there is a particularly simple formula, called McKinsey formula: ◻⋄p→⋄◻p. It is so simple, yet it defines a frame property which cannot be expressed in first-order logic.

Also, with the right selection of other formulas, it gives rise to frame incompleteness examples (logics that are consistent, but are not logics of any class of frames whatsoever).

Answer 67

In combinatorics there are very simple basic graphs from which a whole lot of theory came. For example the complete graphs $K_5$ and $K_{3,3}$ which alone provide the ground level for any non-planar graph according to Kuratowski's theorem. Another simple graph that gave rise to a huge amount of theory is Petersen's graph, which I like to think as the graph whose vertices are the ten two-element subsets of $\{1,2,3,4,5\}$, and for which two such vertices are connected iff they are disjoint.

A link for Kuratowski's theorem is http://en.wikipedia.org/wiki/Kuratowski's_theorem

Answer 68

The Möbius strip or Möbius band (a surface with only one side and only one boundary component).

Answer 69

SLE - stochastic Loewner evolution (or Schramm-Loewner evolution) is a one parameter class of random planar curves. These random curves depend on a real parameter kappa, they are (almost surely) simple curves when kappa is at most 4, they fill the plane when kappa is at least 8. They are related to many planar stochastic models. Look here for more pictures.

^(source)

Answer 70

RSA

(From the Wikipedia article) In cryptography, RSA (which stands for Rivest, Shamir and Adleman) is an algorithm for public-key cryptography. It is the first algorithm known to be suitable for signing as well as encryption, and was one of the first great advances in public key cryptography. RSA is widely used in electronic commerce protocols, and is believed to be secure given sufficiently long keys and the use of up-to-date implementations.

Answer 71

Hyperbolic toral automorphisms (viz. the cat map and its generalizations) are the fundamental examples of Anosov diffeomorphisms, and their suspensions are the fundamental examples of Anosov flows. This is because they are "structurally stable", i.e. small perturbations preserve the Anosov property and any Anosov diffeomorphism on a torus is topologically conjugate to a hyperbolic toral automorphism. I am actually not even aware of any other concrete examples of Anosov dynamics other than those derived from geodesic flows on hyperbolic spaces.

Answered by Steve Huntsman

Answer 72

Turing machines (1937) and Boolean circuits: the primary models for digital computers.

Universal Quantum computers, and quantum Turing machines (Deutsch, 1985).

Answer 73

Borromean rings

Borromean rings are important in several places. For example, they appear in computations of homotopy groups of the 2-sphere, where they corresponds to the Hopf fibration.

Answer 74

Within the category of algorithms and computer science, I would say Conway's "The Game of Life", where binary, two dimensional structures may evolve, requiring not much than an initial state.

http://en.wikipedia.org/wiki/Conway%27s_Game_of_Life

Cellular automatons have spawn practically a branch of computer science on its own right, and has deep connections with dynamical systems and some types of fractals as well, like Sierpinsky's triangle, using rule 90 (in Mathematica):

ArrayPlot[CellularAutomaton[90, {{1}, 0}, 50]] This commands embeds the running of the Rule 90 for 50 steps, from a single 1 on a background of zeros, and then displays Sierpinsky's triangle.

Also, celullar automatons, inspired on the Game of Life, have met their usage as well to study pseudo-randomness, or artificial music (see Stephen Wolfram's work, for example).

Answer 75

Heisenberg model of 1-D chain of spin 1/2 atoms, solved exactly by Bethe in 1931, is where Bethe Ansatz was born, and with it the field of integrable models in statistical and quantum mechanics.

Answered by Mio

Answer 76

The gamma function is a fundamental example of an interesting function defined only on the integers which has an analytic (meromorphic) continuation to the whole complex plane. This ability to extend an interesting, seemingly discrete function to a complex differentiable function motivates a lot of later material.

Answered by Davidac897

Answer 77

Poincare dodecahedral sphere, the 1904 example of a homology sphere was fundamental for the discovery of the fundamental group, and have led to the statement of the Poincare conjecture.

Answer 78

The cone of positive semidefinite matrices is a fundamental example of a convex cone which is important in convexity and for convex and semidefinite programming.

The Reuleaux triangle is the first and most famous example of a set of constant width other than the circle (or ball in higher dimensions).

Answer 79

The pseudo-arc in continuum theory.

Answer 80

I think polynomials are one of the greatest inventions of humankind. Not only are they extremely flexible and come up in so many domains of math, but they've lead to interesting breakthroughs. For example, trying to find a closed formed solution to the quintic polynomial lead Galois to develop groups, right?

Answered by Dagit

Answer 81

While the group of permutations (and permutation matrices) is probably too fundamental to be included, a mysterious, with much more yet to be understood generalization called alternating sign matrices are important in modern combinatorics. Those are square matrices with entries 1, 0 and -1 so that the non zero entries in each row and column alternate in sign and sum up tp one. There is a simple correspondence between alternating sign matrices and monotone triangles.

Answer 82

Schwarzschild metric as a prototype of black hole was a fundamental example in the development of General Relativity (for instance, it is often referred to when "defending" the ADM mass as a natural concept of mass in General Relativity).

Answer 83

Tic-Tac-Toe tends to be the starting example in combinatorial game theory, just because it's simple enough to depict the entire tree on one page yet can still be used to illustrate the standard definitions and notation.

Answer 84

The Alexander polynomial in knot theory.

Answer 85

Motivated by Amit Kumar Gupta's answer about the continuum hypothesis, let me add an example that is less natural but has inspired an amazing amount of set theory, namely Suslin's Hypothesis. This conjecture, proposed in 1920 and now known to be independent of ZFC, says that the real line with its usual ordering relation is characterized up to isomorphism by the following properties:

• dense linear order without endpoints

• Dedekind-complete

• No uncountable family of pairwise disjoint open intervals.

The point of the conjecture is that it was proved much earlier by Cantor that one gets a characterization of $\mathbb R$ if one puts in place of the last property the stronger statement that there is a countable dense set. So Suslin is simply asking whether one can weaken this separability assumption to the third property in the list above (often called the "countable chain condition"). I can't claim that this question is anywhere near as natural as the continuum hypothesis, but what makes it important (in my opinion) is its impact on the development of set theory. The fact that Suslin's hypothesis is false in Gödel's constructible universe $L$ was one of the first applications (and probably a major motivation, though I don't actually know that) for Jensen's theory of the fine structure of $L$, a theory that has grown tremendously as a component of the inner model program in contemporary set theory. The fact that Suslin's hypothesis is consistent with ZFC was the initial application and the motivation for the theory of iterated forcing, now a central tool in set theory. It also provided the occasion for the invention of Martin's axiom. That axiom and the combinatorial principles isolated by Jensen from the fine structure of $L$ have become standard tools for proving independence results without explicitly referring to forcing or to $L$.

Answer 86

Young tableaux and Schur polynomials

Answer 87

The symmetric and alternating groups are fundamental examples in group theory, representation theory, and combinatorics.

Answer 88

I presented the emerging list of examples over my blog and several people suggested a few more examples. I will mention them together:

Tom LaGatta proposed to add the percolation model (1854), John Sidles made several suggestions and in particular proposed several examples from Control theory such as the Nyquist criteria, Christian Blatter proposed adding the Peano curve, and Mark Meckes proposed adding the fundamental Banach spaces L_p/l_p and C(K).

Joe Malkevich proposed several basic examples of games in addition to the prisoner dilemma (chicken, chain store game, and centipede) and the Gale-Shapley model of two-sided market model (the model in the famous Gale-Shapley stable marriage theorem). I thought that we should probably add a basic economic model of exchange markets (like the Arrow-Debreu model).

I also thought the configurations of Desargues and Pappus should be added.

There was also some critique on the classification of examples, and an interesting suggestion By Michael Nielsen that "Distilled and expanded, it could form the basis for an excellent book. Perhaps: 'Examples from the book'." (This refers to Aigner and Ziegler's book "Proofs from the book". (In fact, a similar idea by Ziegler and me have motivated the question itsef.)

Answer 89

The free group factors $L(\mathbb{F}_{n})$, which are the closer in the weak operator topology of the left regular representation of the free group $\mathbb{F}_n$, are fundamental examples in von Neumann algebras. The isomorphism question is the root of the so important Free Probability theory of Voiculescu.

Answer 90

The Newton-Raphson method. A method for finding successively better approximations to the zeroes of a real-valued function. See also this link.

Answer 91

The Lorenz system of ordinary differential equations: $$\dot x=\sigma(y-x)$$ $$\dot y = rx-y-xz$$ $$\dot z = xy-bz$$ ($\sigma$, $r$, $b$ are parameters) is a good example in dynamical system. It is an example of a deterministic system displaying chaotic behaviour. Also the Lorenz attractor. Date: 1963.

Answer 92

Dirichlet Function is a fundamental example in Calculus where Riemann integral does not work. It is also a function which is discontinuous everywhere. The function D(x) is defined as D(x) = 1, if x is a rational number; otherwise D(x) = 0.

For more information, see for example: http://mathworld.wolfram.com/DirichletFunction.html

Answer 93

The Prüfer p-group is a noteworthy example in the theory of Infinite Abelian Groups. (Answer by J. H. S.)

Answer 94

The Ising model (1925)

Answer 95

Three related fundamental examples in random matrix theory (in mathematical physics and probability) are the Gaussian Orthogonal Ensemble, the Gaussian Unitary Ensemble, and the Gaussian Symplectic Ensemble. Much of random matrix theory has been devoted to determining the properties of these families of random matrices and proving that other families exhibit the same behaviors.

Answer 96

Linear Algebra: In linear algebra the symmetric group $S_n=Bij(\{1,,n\})$ is a classical and important example if you learn basics in group theory.

Operator-algebra/ functional-analysis: Fundamental examples of $C^*$-algebras are $C(X)$ ( continuous functions on a compact Haudorff space X), $C_0(X)$ ( continuous functions vanishing at infinity on a localcompact Haudorff space X), $B(H)$ (bounded linear maps on a Hilbert space H). By Gelfand-Naimark you know a lot of abstract $C^*$algebras if you know these concrete examples.

Answer 97

In Combinatorics, the Dyck paths (systems of bracketings, theory of languages, group codes) and Motzkin paths (systems of bracketings, theory of languages, continued fractions). Particular cases of
Lattice paths.

Answer 98

Category theory: There is an isomorphism between a vector space and its double-dual which does not depend on choice of basis. It is natural in the sense that every vector space has such an isomorphism, and these isomorphisms commute with every linear transformation.

This should be contrasted between the isomorphisms between a finite-dimensional vector space and its dual. These depend on a choice of basis and are not natural in this sense.

This example constitutes the first two paragraphs of the first paper in category theory! Eilenberg-Mac Lane: General theory of natural equivalences.

In Categories for the working mathematician, Mac Lane writes that the purpose of discussing categories is to discuss functors, and that the purpose of discussing functors is to discuss natural transformations.

Answer 99

Weierstrass's example of a continuous, nowhere differentiable real function -- apparently was a real surprise at the time and is still surprising to students.

Answer 100

The existence of dense open sets of small measure -- very counterintuitive and allows for all sorts of mischief.

Answer 101

In number theory: the diophantine equation

$a^2-b^3=c$.

This equation can be seen as an epitome of modern number theory, despite its deceptive simplicity.

This equation is not 'fully' understood to this day. But much about it is understood.

This equation is a recurring theme in the award-winning article

Graham Everest, Tom Ward: A Repulsion Motif in Diophantine Equations. The American Mathematical Monthly, vol. 118, no. 7, August-September 2011, pp. 584-598.

Answer 102

The cyclotomic field $\mathbb{Q}(\zeta_p)/\mathbb{Q}$ is the most basic example of a field extension in which splitting of primes depends on an obvious congruence condition. Specifically, if $\ell$ is another prime, then the Frobenius of $\ell$ is $\ell \mod p \in (\mathbb{Z}/p)^\times = \mathrm{Gal}(\mathbb{Q}(\zeta_p)/\mathbb{Q})$. In particular, $\ell$ splits in the field iff its Frobenius is trivial, and this is true iff $\ell \equiv 1 \mod p$. We can then relate other congruences to splitting in subfields of $\mathbb{Q}(\zeta_p)$, etc. The theorems of global class field theory show that this basic concept holds in a very general case, although the general case is much harder to prove. This basic example, does, however, motivate the ideas in class field theory, which have greatly influenced modern number theory and related areas. (As an added note, the fact that the Artin reciprocity law is true for cyclotomic fields is actually a key ingredient in the proof for general abelian extensions!)

Answered by Davidac897

Answer 103

To make this question and the various examples a more useful source this is a designated answer to point out connections between the various examples we collected. please indicate only strong, definite, nontrivial, and clear connections.

1) The Petersen graph is obtained by identifying antipodal vertices and edges in the graph of the dodecahedron - one of the five platonic solids. Such an identification gives a polyhedral complex realizing the real projective plane. Applying this operation to the icosahedron leads to a 6-vertex triangulation of the real projective plane.

Answer 104

Margulis's expanders: This class of 8 regular graphs is the first explicit example for a family of expanders. The vertices are pairs of integer modulo m, the neighbors of (x,y) are (x+y,y), (x-y,y), (x,y+x), (x,y-x), (x+y+1,y), (x-y+1,y), (x, y+x+1), (x,y-x+1). All operations are modulo m.

Expanders were first discovered and constucted probabilistically by Pinsker. The Ramanujan graphs of Lubotzky, Philips and Sarnak are expanders with extremely good properties. This paper by Hoory, Linial and Wigderson contains much more information.

Answer 105

The semicircular law and the Marchenko-Pastur distribution are fundamental examples of probability distributions in random matrix theory.

Answer 106

The hyperfinite $\mathrm{II}_1$ factor $\mathcal{R}$ and its ultrapower $\mathcal{R}^{\omega}$ are fundamental examples in von Neumann algebras and Connes' embedding problem.

Answer 107

In $C^*$-algebras, the Cuntz Algebra is a fundamental example of a separable unital $C^*$-algebra. Its appearance has reshaped much of the theory of $C^*$-algebras.

Answer 108

The image of a torus embedded in $\mathbb{R}^3$ tilted on its side is the fundamental example of Morse Theory. In some sense it shows why you should "believe" all of the Morse lemmas before you sit down to prove them.

Answer 109

I think the question of whether or not $li(x) := \int_{2}^{x} \frac{dt}{\ln(t)}$ was contained in $\mathbb{C}\left(x, \ln\left(x\right)\right)$ spawned the field of galois theory of differential equations. One key question in this field, is what sort of extensions arise from adjoining solutions to a differential equation with coefficients in some ring (for example $\mathbb{C}(x)$?

In the case of the original question it can be posed as what extension arises from the differential equation $$\ln(x)y' = 1?$$

This field developed in parallel to galois theory of number fields (and other algebraic geometry, and arithmetic geometry). A good reference for the field is the aptly titled "Galois Theory of Linear Differential Equations" by Marius Van der Put and Michael Singer.

Answer 110

Theorem on Friends and strangers in Ramsey Theory.

Answer 111

Some of the examples above have indeed shaped whole "disciplines" but others, as striking as they are, are less sweeping in scope.

For me, a very important and thought provoking example, and historically important for a variety of reasons is the Tutte graph. This graph shows a 3-valent 3-polytopal graph which has no hamiltonian circuit. This example, in particular, doomed attempts to prove the 4-color theorem based on ideas related to hamiltonian circuits.

http://en.wikipedia.org/wiki/Tutte_graph

http://mathworld.wolfram.com/TuttesGraph.html

It inspired a great variety of conjectures and work related to hamiltonian circuits for polytopes.

Answer 112

The example that launched category theory: (co)homology, for example simplicial homology and Čech cohomology. The various maps linking (co)homology groups for different 'resolutions' of a topological space (by triangulation or open sets resp.) were I think the first examples of natural transformations. This necessitated defining functors, and hence defining categories.

Answer 113

The discovery of Transcendental numbers, or numbers that are not the root of any finite polynomial with rational coefficients.
Also, the proof that e and π were transcendental, the latter via the proof that e^a is only algebraic for transcendental values of a (and e^*i*π = -1 is algebraic, as is i, so therefore π must be transcendental). Their discovery, as well as the first explicitly created example, the Liouville number, sparked what's called "Transcendence theory".
And as it turns out, any randomly chosen real number is "almost surely" transcendental. In other words, the density of transcendental numbers among the real numbers is 1!!

Answer 114

$\mathbb{Q}_{p}$. The field of p-adic numbers brings the study of local methods. Hensel's lemma is a great example. It is also interesting that p-adic integers is the projective limit of the rings $\mathbb{Z}/p^{n}\mathbb{Z}$.

Answer 115

The (complex analytic) proof of the Prime Number Theorem is the first major use of complex analysis to prove results about asymptotic behavior of prime numbers, which, at first glance, do not at all seem to be tied to complex numbers. This has led to an enormous amount of mathematics.

Answer 116

The field extension $\mathbb{Q}(\sqrt[3]{2})/\mathbb{Q}$ is the most basic example of an algebraic extension which is not Galois. In particular, one notices that it has no non-trivial automorphisms, and that this is related to the fact that not enough of the roots of $x^3-2$ are in this field. This leads to the key concept of Galois extensions and the relation between automorphisms and roots. It also led Galois to develop the concept of normal subgroup.

Answer 117

Ravi Vakil gives interesting examples in algebraic geometry: "The existence of some of these pathologies is ``common knowledge'', but I had never known what they were.".

Answer 118

I think no one's pointed Lorenz equations.

Answer 119

to understand curves, first study the abel map. and then the torelli map. [perhaps I should expand this rather succinct answer.]

8320 Spring 2010, day one Introduction to Riemann Surfaces

We will describe how Riemann used topology and complex analysis to study algebraic curves over the complex numbers. [The main tools and results have analogs in arithmetic, which I hope are more easily understood after seeing the original versions.]

The idea is that an algebraic curve C, say in the plane, is the image by a holomorphic map, of an abstract complex manifold, the Riemann surface X of the curve, where X has an intrinsic complex structure independent of its representation in the plane. Then Riemann's approach to classifying all complex curves, is to classify such Riemann surfaces, and then for each such surface to classify all maps from it to projective space. Briefly, the Torelli maps classifies complex surfaces, and the abel maps classify all projective models of a given complex surface.

More precisely, we will construct two fundamental functors of an algebraic curve:

i) the Riemann surface X, and

ii) the Jacobian variety J(X), and

natural transformations X^(d)--->J(X), the Abel maps, from the “symmetric powers” X^(d) of X, to J(X).

The Riemann surface X

The first construction is the Riemann surface of a plane curve: {irreducible plane curves C: f(x,y)=0} ---> {compact Riemann surfaces X}.

The first step is to compactify the affine curve C: f(x,y) =0 in A^2, the affine complex plane, by taking its closure in the complex projective plane P^2. Then one separates intersection points of C to obtain a smooth compact surface X. X inherits a complex structure from the coordinate functions of the plane. If f is an irreducible polynomial, X will be connected. Then X will have a topological genus g, and a complex structure, and will be equipped with a holomorphic map ƒ:X--->C of degree one, i.e. ƒ will be an isomorphism except over points where the curve C is not smooth, e.g. where C crosses itself or has a pinch.

This analytic version X of the curve C retains algebraic information about C, e.g. the field M(X) of meromorphic functions on X is isomorphic to the field Rat(C) of rational functions on C, the quotient field k[x,y]/(f), where k = complex number field. It turns out that two curves have isomorphic Riemann surfaces if and only if their fields of rational functions are isomorphic, if and only if the curves are equivalent under maps defined by mutually inverse pairs of rational functions.

Since the map X--->C is determined by the functions (x,y) on X, which generate the field Rat(C), classifying algebraic curves up to “birational equivalence” becomes the question of classifying these function fields, and classifying pairs of generators for each field, but Riemann’s approach to this algebraic problem will be topological/analytic.

We already can deduce that two curves cannot be birationally equivalent unless their Riemann surfaces have the same genus. This solves the problem that interested the Bernoullis as to why most integrals of form dx/sqrt(cubic in x) cannot be “rationalized” by rational substitutions. I.e. only curves of genus zero can be so rationalized and y^2 = (cubic in x) usually has positive genus.

The symmetric powers X^(d)

To recover C, we seek to encode the map ƒ:X--->C, i.e. ƒ:X--->P^2, by intrinsic geometric data on X. If the polynomial f defining C has degree d, then each line L in the plane P^2 meets C in d points, counted properly. Thus we get an unordered d tuple of points L.C, possibly with repetitions, on C, hence when pulled back via ƒ, we get such a d tuple called a positive “divisor” D = ƒ^(-1)(L) of degree d on X. (D = n1p1+...nk pk, where nj are positive integers, n1+...nk = d.)

Since lines L in the plane move in a linear space dual to the plane, and (if d ≥ 2) each line is spanned by the points where it meets C, we get an injection P^2*--->{unordered d tuples of points of X}, taking L to ƒ^(-1)(L).

If X^d is the d - fold Cartesian product of X, and Sym(d) is the symmetric group of permutations of d objects, and we define X^(d) = X^d/Sym(d) = the “symmetric product” of X, d times, then the symmetric product X^(d) parametrizes unordered d tuples, and inherits a complex structure as well.

Thus the map ƒ:X--->C yields a holomorphic injection P^2*--->Π of the projective plane into X^(d). I.e. the map ƒ determines a complex subvariety of X^(d) isomorphic to a linear space Π ≈ P^2*. Now conversely, this “linear system” Π of divisors of degree d on X determines the map ƒ back again as follows:

Define ƒ:X--->Π* = P^2** =P^2, by setting ƒ(p) = the line in Π consisting of those divisors D that contain p. Then this determines the point ƒ(p) on C in P^2, because a point in the plane is determined by the lines through that point. [draw picture] Thus the problem becomes one of determining when the product X^(d) contains a holomorphic copy of P^2, or copies of P^n for models of X in other projective spaces.

The Jacobian variety J(X) and the Abel map X^(d)--->J(X).

For this problem, Riemann introduced a second functor the “Jacobian” variety J(X) = k^g/lattice, where k^g complex g -dimensional space. J(X) is a compact g dimensional complex group, and there is a natural holomorphic map Abel:X^(d)--->J(X), defined by integrating a basis of the holomorphic differential forms on X over paths in X.

Abel collapses each linear system Π ≈ P^n* to a point by the maximum principle, since the coordinate functions of k^g have a local maximum on the compact simply connected variety Π. Conversely, each fiber of the Abel map is a linear system in X^(d). Existence of linear systems Π on X: the Riemann - Roch theorem.

By dimension theory of holomorphic maps, every fiber of the abel map X^(d)--->J(X) has dimension ≥ d-g. Hence every positive divisor D of degree d on X is contained in a maximal linear system |D| , where dim|D| ≥ d-g. This is called Riemann’s inequality, or the “weak” Riemann Roch theorem.

The Roch part analyzes the relation between D and the divisor of a differential form to compute dim|D| more precisely. Note if D is the divisor cut by one line in the plane of C, and E is cut by another line, then E belongs to |D|, and the difference E-D is the divisor of the meromorphic function defined by the quotient of the linear equations for the two lines.

If D is a not necessarily positive divisor, we define |D| to consist of those positive divisors E such that E-D is the divisor of a meromorphic function on X. If there are no such positive divisors, |D| is empty and has “dimension” equal to -1. Then if K is the divisor of zeroes of a holomorphic differential form on X, the full Riemann Roch theorem says:

dim|D| = d-g +1+dim|K-D|, where the right side = d-g when d > deg(K).

This sketch describes the abel maps and their relation to the RRT. The assignment X-->J(X) is the Torelli map, and classifies X by the numerical data in the lattice defining J(X), i.e. periods of integrals of the first kind on X. This assignment gives birth to the whole subject of "moduli" as numerical invariants of complex or geometric structure.a

Answer 120

$\aleph_\omega$

I suppose that $\aleph_0$ and $2^{\aleph_0}$ are, like the natural numbers and the unit ball, "too fundamental" as they are fundamental for mathematics as a whole. But the $\omega^{\mathrm{th}}$ cardinal, $\aleph_{\omega}$ already suits us as a fundamental object in set theory and infinite combinatorics.

Can you show that the continuum is NOT $\aleph_{\omega}$ ?

Answer 121

Although this may fall foul of the criticism that it perhaps it has not shaped a subject yet, I'll give it the benefit of the doubt that it may still shape a future subject. In a way the answer touches two answers already given: the Platonic solids and also the quaternions.

I am talking about the ADE classification, which appears in the theory of Lie algebras, finite subgroups of $SU(2)$ (McKay correspondence), representation theory of quivers (Gabriel's theorem), singularity theory (Du Val), classification of conformal field theories,...

Answer 122

The arithmetics of conics with pythagorean triples is since long been used as toy model for the beautifull combination of arithmetics, analysis and geometry in the study of algebraic curves, but Lemmermeyer's "Conics - a Poor Man's Elliptic Curves" and his subsequent arxiv articles pushes the "toy" into the direction of a "fundamental example" for some fascinating issues.

Answer 123

Spheres (of various dimensions) are the fundamental examples of (compact) Riemannian manifolds (or even Alexandrov spaces) of curvature > 0. Several major theorems of Riemannian geometry were motivated by the question of how to recognize a sphere. Most recently this culminated in Brendle and Schoen's proof of the differentiable sphere theorem.

Answer 124

The Thompson groups, as wikipedia said, have a collection of unusual properties which have made them counterexamples to many general conjectures in group theory. For example it is a finite generated finite presented torsion free group with infinite cohomology dimension. For more information see: http://en.wikipedia.org/wiki/Thompson_groups

Answer 125

I suppose the discrete metric space is a crucial example in the metric spaces theory and in the introductory mathematical analysis. It shows many aspects and pathological behavior of metric spaces in general.

Answer 126

Taking introductory topology, I got the impression that the real line is the fundamental example of a topological space. I wouldn't be surprised if the open and closed intervals of $\mathbb{R}$ were the prototypical examples of open and closed sets, and I think many important topological properties---including compactness, connectedness, and Hausdorffness---first arose because you need them to prove obvious facts about $\mathbb{R}$ and its subsets.

Answer 127

The parallel-or functional is a fundamental example in denotational semantics.

Answer 128

The field of Hyperbolic Systems of Conservation Laws has a paradigm : the Euler equations of an inviscid compressible gas. For those interested, these are the conservation of mass, momentum and energy: $$\partial_t\rho+{\rm div}(\rho u)=0,$$ $$\partial_t(\rho u)+{\rm Div}(\rho u\otimes u)+\nabla p(\rho,e)=0,$$ $$\partial_t(\frac12\rho|u|^2+\rho e)+{\rm div}((\frac12\rho|u|^2+\rho e+p)\rho u)=0,$$ where $\rho$ is the mass density, $u$ the flow velocity, $e$ the specific internal energy and $p$ the pressure, given by an equation of state.

Riemann wrote a deep paper on the $1$-dimensional isothermal (drop the last equation, take $p=A^2\rho$) case, after which the Riemann problem and the Riemann invariants have been coined.

Answer 129

The lady tasting tea: https://en.wikipedia.org/wiki/Lady_tasting_tea was a fundamental example introducing the idea of significance tests.

Answer 130

The Hawaiian earring, the union of a null sequence of circles joined at a common point.

1) Shows that a connected, locally path connected metric space can fail to be locally contractible.

2) (Much less obvious). Amplifies the failure of TOP as the `correct' category in which to do algebraic topology. For example the fundamental group of the Hawaiian earring (with the natural quotient topology inherited from the space of based loops) fails to be a topological group in TOP.

(The true source of pathology is not the Hawaiian earring and its properties, but rather the general failure of quotients and products to commute in the category TOP, (i.e. the quotient of the product might not be the product of the quotients with standard definitions of topological quotients and topological products). Such discrepancy makes the case for the continued relevance of category theory.

Answer 131

Euclid's lemma concerning the infinitude of primes seems fundamental and basic to Number Theory. It also seems to be a catalyst for the many "infinitely many primes of the type...." - problems. Also related is the "reductio ad absurdum" model used to prove the result.

Answer 132

3264 is considered "emblematic" of a solution to an instance of the fundamental problem of constructing notions of 'random objects'/'generic object'/'objects in general position'.

In D. Eisenbud, J. Harris: 3264 and all that. Cambridge University Press (2016) one reads:

"[...] the determination, by Chasles,¹ of the number of smooth conic plane curves tangent to five given general conics. The problem is emblematic of the dual nature of the subject. On the one hand, the number itself is of little significance: [...] But the fact that the problem is well-posed---that there is a Zariski open subset of the space of 5-tuples $(C_1,\dotsc,C_5)$ of conics for which the number of conics tangent to all five is constant, and that we can in fact determine that number---is at the heart of algebraic geometry. And the insights developed [...] [for] a rigorous derivation of the number [...] [e.g.] a new parameter space for plane conics, and the understanding why intersection products are well-defined for this space---are landmarks [...] the number 3264 [...] is as emblematic of enumerative geometry as the date 1066 [...] is of English history."

[emphasis added] The Zariski-openness means that there is a meaningful notion of 'general position'.

An introduction (in French):

Étienne Ghys:TROIS MILLE DEUX CENT SOIXANTE-QUATRE. Comment Jean-Yves a récemment précisé un théorème de géométrie. Images des Mathématiques. 2008

¹ _{Joncquières is said to have obtained this result earlier, yet did not publish. None of the 'solutions' seems to be considered rigorous, and a proof, i.e. a correct deduction of '3264' from respected axioms, had to wait until the late 20th century.}

Answer 133

Dirichlet's theorem is the first use of analysis to prove a number theoretic result which does necessarily seem analytic. His proof leads to a lot of ideas about distributions of primes, many of which used analysis. It even leads to an analytic proof of one of the inequalities in class field theory, a result which can also be proved using a good deal of cohomology and which is therefore not exclusively analytic. (I am not counting the prime number theorem, since that is an asymptotic result and thus reeks of analysis as soon as it is conjectured. It was also proven later.)

Answer 134

Second price auction (or Vickrey auction): an auction in which the bidder who submitted the highest bid is awarded the object being sold and pays a price equal to the second highest amount bid.

Answer 135

Two unrelated examples: The configuration of 27 lines on a cubic surface ; (See also here and here) The regular heptadecagon (17 sides polygon) and its geometric construction.

Answer 136

Surreal numbers

Answer 137

The Delaunay triangulation is fundamental in computational (Euclidean) geometry. For a finite point set S in general position, it can be defined in several ways: (1) as the unique triangulation in which every simplicial cell is Delaunay (i. e., its circumsphere does not contain any points of S in its interior), (2) as the uniqe triangulation in which every facet (of any dimension) of every simplicial cell is Delaunay (meaning it has some empty circumsphere), or (3) as the dual of the Voronoi diagram (which is also fundamental). In the plane, the Delaunay triangulation has the additional property of maximizing the smallest angle of all its triangles, among all triangulations.

The Delaunay triangulation is usually the most obvious candidate for "the right" triangulation of a given point set, and most simplicial mesh-generating methods seem to be based on it. It doesn't hurt that there are reasonably fast and elegant algorithms for constructing it (very fast in the plane, but unfortunately (and necessarily) exponential in the dimension in the worst case).

Answer 138

The solution of Kirkman's Schoolgirl Problem is the archetypal example of a resolvable triple system. This example essential shaped the entirety of Design Theory.

We might also consider Euler's 36 Officers Problem to be one of the fundamental counter-examples within this field. Answer by Disonnant

Answer 139

Fermat hypersurfaces and their Zeta functions.

Udi de Shalit proposed: One example that comes to my mind is the Zeta functions of the Fermat hypersurfaces, which were studied by Weil and are known to have helped him in formulating the Weil conjectures, later on proved by Grothendieck and Deligne.

Answer 140

The most fundamental equation is $x^2+1=0$.