44

Janos Pach asked a deep question 23 years ago (1988) that remains unsolved today:

Can every animal—a topological ball in $\mathbb{R^3}$ composed of unit cubes glued face-to-face—be reduced to a single unit cube by adding and deleting cubes, while always maintaining the animal (ball) property?

("Animal" was an apparently original coinage of Janos's.) I and my students quickly found irreducible animals, i.e. balls of unit cubes from which no cube can be removed without destroying the topological-ball property. Here is one of 119 cubes due to Tom Shermer (which I exploded vertically for visualization):
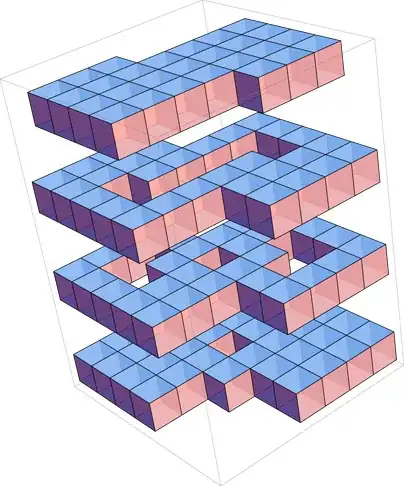
alt text
Essentially all our irreducible examples are based on Bing's House with Two Rooms (unbeknownst to us at the time). So if Pach's question has a positive answer, it requires adding cubes as well as deleting. This history is recounted in Günter Ziegler's Lectures on Polytopes, Springer, 1995, p.276. His non-shellability Theorem 8.15 (p.243) is based on these irreducible animals.

So, I finally come to my question, which is essentially a question of shellability:

Can every (embedded) object constructed by gluing unit cubes face-to-face, regardless of genus, be reduced to a single unit cube by adding and deleting cubes, while always maintaining that the surface is a 2-manifold?

This is exactly Pach's question, but with the ball-requirement removed. All the irreducible animals I know rely on violating the topological-ball requirement for their irreducibility; so it is (remotely) possible that reduction alone suffices(!). I am tempted to introduce a new genera to encompass Plantae & Animalia; but I resist.

Any pointers that may lead me to information on the generalization of Pach's question would be greatly appreciated. Thanks!

Addendum, 11 May 2011 (original posting on 2 January 2011). The problem is now solved (positively): Every animal can be reduced by adding and deleting cubes. The proof is contained in two papers, the second of which appeared as a tech report in May 2010: "A solution to the animal problem," by Akira Nakamura. Here is the PDF. The first paper, an earlier 2006 tech report, is called simply, "B-Problem," by Akira Nakamura, Kenichi Morita, and Katsunobu Imai. Here is its PDF. I would summarize but I do not yet understand the papers, which are presented in terms of "digital topology."

Joseph O'Rourke
  • 149,182
  • 34
  • 342
  • 933
  • Joseph, which program do you use for your graphics? – Andrés E. Caicedo Jan 02 '11 at 23:15
  • @Andres: The color scheme looks like Mathematica(tm) – Igor Rivin Jan 02 '11 at 23:19
  • @Andres: Thanks for asking; I am eclectic :-). That image was produced in Mathematica, whereas the Christmas tree balls in http://mathoverflow.net/questions/50150/light-reflecting-off-christmas-tree-balls and the Thurston reflex-hull image in http://mathoverflow.net/questions/39378/the-reflex-free-hull-construction were constructed in POV-ray. (continued...) – Joseph O'Rourke Jan 02 '11 at 23:32
  • ... I often use Adobe Illustrator, e.g, http://mathoverflow.net/questions/50800/finding-points-inside-innermost-convex-hull/50813#50813, and sometime, raw Postscript: http://mathoverflow.net/questions/38307/trapped-rays-bouncing-between-two-convex-bodies/38314#38314 . Jack of all trades; master of none. :-) – Joseph O'Rourke Jan 02 '11 at 23:33
  • 1
    1988 + 13 = 2001 – Petya Jan 03 '11 at 03:26
  • 1
    If you use a cell division of space that has 4 cells touching each vertex in place of the cubical subdivision, then this particular question becomes trivial: every union of cells has boundary a manifold.

    Is much known about other cell divisions, for instance the tiling by associated with the tetrahedral reflection group where the tetrahedron has two opposite 90 degree angles and all other angles 60 degrees?

     – Bill Thurston Jan 03 '11 at 16:53
  • 1
    @Bill: Good questions, and I am afraid I know little. I do recall that Krystyna Kuperberg proved something like this: If every cube is replaced by $k^3$ cubes, then the answer to Pach's question is 'Yes.' I believe she established this for $k=3$. – Joseph O'Rourke Jan 03 '11 at 21:34
  • 1
    The term animal or lattice animal is a common term for these creatures (polyominoes, polycubes, etc.) in the physics literature. – Günter Rote Sep 24 '17 at 11:49
  • 2
    I would only write that an alleged proof was announced, but it was never published, or confirmed to be valid by anyone else. Also, the links to the manuscripts are broken. – domotorp Feb 15 '22 at 08:01

1 Answers1

7

Regarding Pach's original question: Bing's house deals with the analogous question of collapsibility. It is an example of a contractible non-collapsible space. For that problem it is known that if you allow both collapses and anti-collapses, every contractable space can be reduced to a point. This follows from "Simple homotopy theory". I dont know if this result of simple homolopy theory extends to animals built from cubes but they might.

The modified higher genus question seems easier since you allow steps that changes the topology of the animal.

One can ask a stronger question if when you fixed the genus g you can pass between two animals of genus g by such steps. The analogous question for collapsibility seems to relate to simple homotopy invariants of surface groups but I dont know what they are.

Gil Kalai
  • 24,218