6

Hello, I am interested in some kind of sequence that are "not finitely recurrent".

Let $a_i$ be a sequence taking values in $\{0,1\}$. Consider the sequence $(u_i)$ such that $u_0=1$, and for any positive integer $n$, $u_n =\sum_{i=1}^n u_{n-i}a_i$

It is easy to prove that there exists some positive term $\lambda$ such that $(u_n)$ growth faster than $(\lambda-\epsilon)^n$ and slower than $(\lambda+\epsilon)^n$ for any $\epsilon>0$. I would like to know if it is possible to get better bounds, even by adding if necessary some hypothesis on the coefficients $(a_i)$ (but of course this should not be a periodic sequence, otherwise this is well known and too easy).

Thanks by advance for your comments !

J.C. Ottem
  • 11,519
Nekochan
  • 449
  • 3
  • 10

1 Answers1

4

Let me slightly change the notation. You have some sequence $\mathbf{a}=a_0,a_1,\cdots$ with each $a_i$ either $0$ or $1$. Define a sequence $u_0,u_1,u_2,\cdots$ by setting $u_m=0$ for $m \lt 0$, $u_0=1$ and for any $n \ge 0$, $u_{n+1}=\sum_{i=1}^{\infty}a_iu_{n-i}.$ As you note in a comment, if $a_1=1$ then $u_i$ is a non-decreasing and eventually increasing sequence (excluding a trivial case). The sequence $u_i$ will eventually be increasing as long as the set of $j$ with $a_j=1$ has a $\gcd$ of $1$.

Consider the power series $f(r)=r-(a_0+\frac{a_1}{r}+\frac{a_2}{r^2}+\cdots).$ Then $f(r)$ is defined and increasing for $r \gt 1.$ There is a unique $\lambda=\lambda_{\mathbf{a}}>1$ with $f(\lambda)=0.$ I think that there should be a constant $c \le 1$ with $\lim \frac{a_n}{c\lambda^n}=1$. We can also say that $\lambda \le 2$ with equality only in the degenerate case that $a_i=1$ for all $i$. For any $1 \lt r \lt 2$ we can create an $\mathbf{a}$ with $\lambda_{\mathbf{a}}=r$ by simply choosing the $a_i$ one at a time to keep the (non-decreasing) partial sums of $f(r)$ non-negative.

We can partially order the possible sequences $\mathbf{a}=(a_i)$ by saying $\mathbf{a}<\mathbf{b}$ when $a_i=b_i$ for $0 \le i \lt j$ and $0=a_j<b_j=1.$ In this case, $\lambda{\mathbf{a}}<\lambda_{\mathbf{b}}$.`

In case $a_i=0$ from some point on we know how to find $\lambda$ as the root of a polynomial and if $a_i=1$ from some point on we again know how to find $\lambda$ as the root of a polynomial (perhaps with a coefficient equal to $2$.So this gives us both a lower bound and an upper bound on $\lambda_{\mathbf{a}}$ based on any initial portion of $\mathbf{a}.$

I'll stop there for now although probably more can be said.

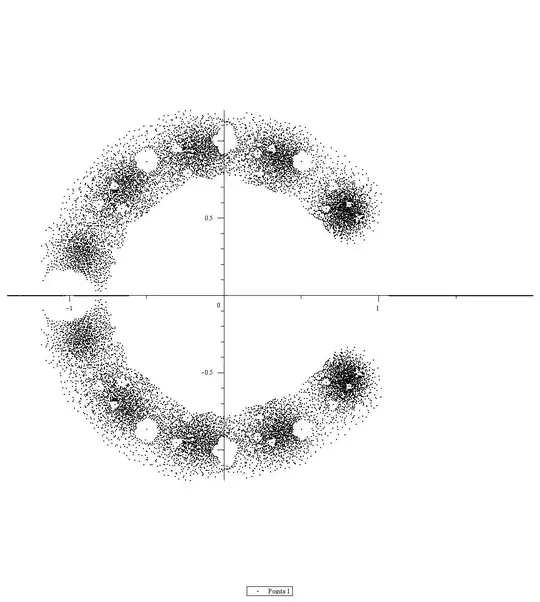
Consider the $2^d$ sequences $\mathbf{a}$ with $a_{d+m}=0$ for $m \gt 0.$ If all the roots, real and complex , of $f(r)$ are plotted then you should get a picture something like the one below. This plot is for $d=12$ you can see a similar one at this question

enter image description here

Community
  • 1
Aaron Meyerowitz
  • 30,015
  • Thanks for your reply!

    Actually, I have forgotten to add the hypothesis $a_1=1$ so that we get a non-decreasing sequence. The kind of asymptotic behaviour you suggest is very interesting. However, I have no idea of an explicit sequence that match this behaviour.

    Maybe there could exist some connection with the eigenvalues of some compact operator, so that the growth rate would not be $f(n) \lambda^n$ but a converging series $\underset{k}{\sum} f_k(n) \lambda_k^n$, the $f_k$ being polynomials with "good properties" (dunno exactly what this means...) and such that $(\lambda_k)_k$ tends to 0.

     – Nekochan Apr 20 '11 at 17:14