Shortest closed curve to inspect a sphere

Question

Let $S$ be a sphere in $\mathbb{R}^3$. Let $C$ be a closed curve in $\mathbb{R}^3$ disjoint from and exterior to $S$ which has the property that every point $x$ on $S$ is visible to some point $y$ of $C$, in the sense that the segment $xy$ intersects $S$ at precisely the one point $x$. I am interested in the shortest $C$ with this property. In computational geometry, such paths are called watchman tours, and there are many results concerning polygons in the plane finding such tours.

This question arose at a conference I'm attending, and I was pointed to a paper by V. A. Zalgaller:

"Shortest Inspection Curves for the Sphere" (Journal of Mathematical Sciences, Volume 131, Number 1, 5307-5320; Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 299, 2003, pp. 87–108.)

I cannot access the paper from the conference, but from the abstract it appears he focused on open rather than closed curves.

Has anyone heard of this natural question? Can you point me to relevant literature? Thanks!

Addendum. Here is the $4\pi$ saddle / baseball-stitches curve suggested by Gjergji Zaimi:
          

Answer 1

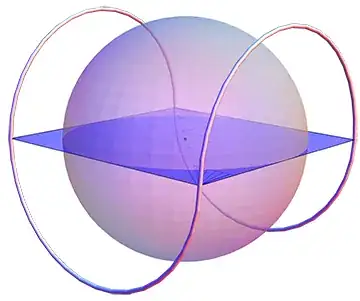
James Wenk and I just finished a paper proving Zalgaller's sphere inspection conjecture for closed curves:

Shortest closed curve to inspect a sphere.

We show that in $R^3$ any closed curve $\gamma$ which inspects the unit sphere $S^2$, i.e., lies outside $S^2$ and contains $S^2$ within its convex hull, has length $L(\gamma)\geq 4\pi$. Equality holds only when $\gamma$ is composed of 4 semicircles of length $\pi$, arranged in the shape of a baseball seam, as conjectured by Zalgaller in 1996.

The proof, which runs 38 pages, uses some notions from the earlier work on this problem which I had mentioned in my last post below, together with other ideas from integral geometry, convex analysis, geometric measure theory, and geometric knot theory. Furthermore, we derive a number of formulas for inspection efficiency of curves, which can be verified with the aid of a Mathematica notebook which we have provided. The basic approach is as follows.

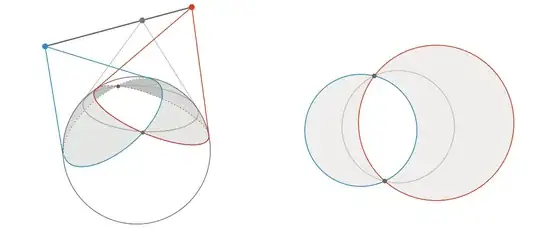
Let $\gamma\colon[a,b]\to R^3$ be a closed rectifiable curve inspecting $S^2$. As I had mentioned in my last post, the horizon of $\gamma$ is defined as $$ H(\gamma):=\int_{p\in S^2} \#\big(\gamma^{-1}(T_pS^2)\big)\, dp, $$ i.e., the measure in $S^2$ of all points $p$ counted with multiplicity where the tangent plane $T_p S^2$ intersects $\gamma$. The horizon of a line segment, for instance, is the area of the region illustrated in the picture above. In the current paper we define the (inspection) efficiency of $\gamma$ as $$ E(\gamma):=\frac{H(\gamma)}{L(\gamma)}. $$ We want to show that $L(\gamma)\geq 4\pi$. Since $\gamma$ is closed, $H(\gamma)\geq 8\pi$. So it suffices to show that $E(\gamma)\leq 2$. To this end we note that, since $H$ is additive, for any partition of $\gamma$ into subsets $\gamma_i$, $i\in I$, $$ E(\gamma)= \sum_i \frac{H(\gamma_i)}{L(\gamma)}=\sum_i \frac{L(\gamma_i)}{L(\gamma)} E(\gamma_i)\leq \sup_i E(\gamma_i) . $$ So the key to solving the problem would be to construct a partition with $E(\gamma_i)\leq 2$ for all $i\in I$.

To construct the desired partition we may assume that $\gamma$ has minimal length. Then we connect all points of $\gamma$ to the origin $o$ of $R^3$ to obtain a conical surface. This surface can be isometrically developed into the plane to yield a curve $\tilde\gamma\colon[a,b]\to R^2$ which is called the (cone) unfolding of $\gamma$. This operation goes back to a paper of Cantarella, Kusner, and Sullivan on thickness of knots. It turns out that $$ E(\gamma)=E(\tilde\gamma). $$ Furthermore, since $\gamma$ is minimal, it follows that $\tilde\gamma$ is locally convex with respect to $o$. Consequently it admits a partition into segments we call spirals, which are maximal subsets of $\tilde\gamma$ with monotone distance from $o$. We prove that the efficiency of any spiral is at most $2$ which yields the desired inequality $L(\gamma)\leq 4\pi$. The proof is based on a computation of $E$ for line segments, polygonal approximations, and a variational procedure.

The above arguments fill the first half of the paper. The second half is devoted to characterizing the case where $L(\gamma)=4\pi$. This part of the paper gets quite a bit more analytical, and requires more precise estimates for efficiency. The main idea here is that if $L(\gamma)=4\pi$, then $E(\gamma)=2$ which in turn yields that $E(\tilde\gamma_i)=2$ for all the spirals in the unfolding of $\gamma$. We show that $E(\tilde\gamma_i)=2$ only when $\tilde\gamma_i$ has constant distance $\sqrt2$ from $o$, which in turn yields that $\gamma$ must have constant distance $\sqrt2$ from $o$ as well, or lie on a sphere of radius $\sqrt2$. Finally we show that $\gamma$ must be composed of $4$ semicircles using a Crofton type formula of Blaschke-Santalo for length of spherical curves, and a technique from the proofs of the classical $4$ vertex theorem, which has been developed further by Umehara and Thorbergsson.

In short, as had been anticipated at the end of my last post, the proof of the full result did require substantial effort beyond the estimates obtained in the earlier work. Zalgaller's conjectures for open inspection curves still remain unresolved. It is also natural to consider higher dimensional versions of the problem. Some of the techniques discussed above apply in all dimensions, but more ideas would be needed to extend the result.

Update (July 2021): The proof has been simplified and the paper, which has been shortened to 25 pages, has been accepted for publication in Crelle's journal.

Answer 2

I have recently finished a paper called

The length, width, and inradius of space curves

where it is shown that the length $L$ of any closed curve $\gamma\colon[a,b]\to \mathbf{R}^3$ inspecting the unit sphere $\mathbf{S}^2$ must be at least $$ 6\sqrt{3}\approx 10.3923, $$ which is almost $83$% of the conjectured lower bound $4\pi\approx 12.5664$ by Zalgaller and Gjergji Zaimi. This paper discusses a number of ideas and techniques to study the inspection problem, which I will summarize below. Here inradius is the supremum of the radii of all spheres which are contained in the convex hull of $\gamma$ and are disjoint from $\gamma$. It is easy to see that $\gamma$ inspects $\mathbf{S}^2$, up to a translation, if and only if its inradius $r$ is $1$.

---

1. The theorem of Wienholtz. The first approach to the inspection problem, which is also called the inradius problem in the paper, is to study the more basic width problem, i.e., minimizing $L$ subject to a constraint on $w$, the infimum of the distances between all pairs of parallel planes which contain $\gamma$ in between them. Since $$ w\geq 2r, $$ any lower bound for $L/w$ yields a lower bound for $L/r$. To this end, one can apply a beautiful unpublished result of Daniel Wienholtz from 2000 who used the Borsuk-Ulam theorem to show that any closed space curve $\gamma$ may be positioned between a pair of parallel planes $H_0$, $H_1$, which touch $\gamma$ twice each in alternating fashion as one goes around $\gamma$. Let $L_1$ be the length of the projection of $\gamma$ into a line orthogonal to $H_0$, and $L_2$ be the length of the projection of $\gamma$ into $H_0$. Then, since projections do not reduce width, $$ L\geq \sqrt{L_1^2+L_2^2}\geq\sqrt{(4w)^2+(\pi w)^2}=\sqrt{16+\pi ^2}\,w\geq \sqrt{16+\pi ^2}\,2r. $$ So $L/r\geq 2\sqrt{16+\pi ^2}>10.1724$. The first inequality above follows from the Cauchy-Schwartz inequality for integrals, while the second uses Wienholtz's theorem and the Cauchy-Crofton formula, both of which are included in the paper. It is also shown that the inequality $L/w\geq \sqrt{16+\pi ^2}$ is better than $99.43$% sharp. In particular, the length of the shortest closed curve of width $1$ must be approximately $5.1$.

---

2. The notion of horizon. In order to impove the lower bound for $L/r$ we adopt a more direct integral-geometric approach by developing the notion of horizon. The horizon of a curve $\gamma$ is defined as the measure of all tangent planes of $\mathbf{S}^2$ counted with multiplicity which intersect $\gamma$: $$ H(\gamma):=\int_{p\in S^2} \#\big(\gamma^{-1}(T_p S^2)\big)\, dp. $$ Since $\gamma$ is closed and inspects $\mathbf{S}^2$, $H(\gamma)\geq 8\pi$. Next, to derive an upper bound for $H(\gamma)$ we show that for every curve $\gamma$ inspecting $\mathbf{S}^2$ there is another inspection curve $\tilde \gamma$ with length $\tilde L\leq L$ such that the tangent lines of $\tilde\gamma$ do not enter $\mathbf{S}^2$. For these curves one can show that $H(\tilde\gamma)\leq \frac{4\pi}{3\sqrt3}\tilde L$, by studying the following expression for the horizon which we compute using the area formula: $$ H(\gamma)=\int_a^b\int_0^{2\pi} \frac{1}{\|\gamma\|^2}\left| \sqrt{\|\gamma\|^2-1}\sin(\alpha)\cos(\theta)+\cos(\alpha) \right|\,d\theta dt. $$ Here $\alpha$ is the angle betweeb $\gamma$ and $\gamma'$ and we are assuming that $\|\gamma'\|=1$. The tangent line property of $\tilde\gamma$ means that $\sin(\tilde\alpha)\geq 1/\|\tilde\gamma\|$. Now putting everying together we have $$ 8\pi\leq H(\tilde\gamma)\leq \frac{4\pi}{3\sqrt3}\tilde L\leq \frac{4\pi}{3\sqrt3}L, $$ which yields $L\geq 6\sqrt3>10.3923$.

---

3. Other estimates There are some more things one can do via Crofton's formula, which are included in the paper. For instance if $M:=\max\|\gamma\|$, $m:=\min\|\gamma\|$. Then $$ L\geq\frac{2\pi Mm}{\sqrt{M^2-1}}. $$ In particular, when $M=m$, or $M\leq 2/\sqrt3$, then $L\geq 4\pi$. This generalizes the obsevartion by Jean-Marc Schlenker above on inspection curves of constant height. Further, in the paper we study the above integral formula for the horizon via a computer which shows that if $m\geq 1.6$, then $L\geq 4\pi$. Thus if a counterexample to the $4\pi$ conjecture exists, then for some $t\in[a,b]$ we must have $$ 1.15 \leq\|\gamma(t)\|\leq 1.6. $$ Finally the paper describes how the Wienholtz's theorem may be used to extend the above estimates to higher dimensions, but I do not know how sharp these are.

In conclusion let me point out that it is very tempting to think that the inspection problem should have a slick or elegant solution via some kind of integral formula in the style of Crofton-Blaschke-Santalo, and someone might yet see that; but even the proof of the inradius problem for curve segments in the plane (see the paper for references) remains quite long and complicated. So it might turn out that the complete solution to the inspection problem will require substantial effort. Hopefully the ideas and techniques developed in the above paper will help.

Answer 3

The baseball stitches curve suggested by Gjergji Zaimi appears in another paper of Zalgaller:

V. A. Zalgaller. Extremal problems on the convex hull of a space curve. Algebra i Analiz, 8(3):1–13, 1996.

Here Zalgaller also conjectures that this curve should be the minimizer.

Answer 4

In another paper with James Wenk, we have shown that the condition in Zalgaller's conjecture that the curve lie outside the sphere is not necessary, that is, the inequality $L\geq 4\pi$ holds for all closed curves in $R^3$ which contain the sphere in their convex hull, and equality is achieved only by the baseball curve:

Shortest closed curve to contain a sphere in its convex hull

Furthermore, the paper contains an appendix which establishes the estimate $L\geq Cn\sqrt{n}$ by Fedor Nazarov for this problem in $R^n$. This estimate is sharp up to the constant $C$, and is proved using Gauss' correlation inequality. It also leads to a result of Tikhomirov on covering the sphere with congruent disks, see this related post.

Update (March 2024): The paper has been accepted for publication in Bulletin of the London Math. Society.

Answer 5

I am quite sure that the problem is open, but we can play math-sport --- who makes a better constant.

Let me make a long remark, mostly based on the Zalgaller's paper. I will describe a family of examples, which includes the $4{\cdot}\pi$-example of Gjergji Zaimi, but I can not see if $4{\cdot}\pi$ is the best constant in this family. (It seems that you are a friend of computer and it would be easy for you to check.)

The curve can be viewed a $S^1$-family of circles on the sphere. In the example of Gjergji Zaimi, each circle in the family has exactly one point on one half-equator and one on the opposite meridian. Instead of half-equator and meridian one can choose two curves and consider corresponding $S^1$-family of circles; such a pair of curves is described by few parameters. (The centers of the circles in this family also can be described as envelop-line for circles of half-radius in the Zalgaller's family)

Answer 6

We have a recent (much less technical) note regarding the length of the curve inspecting the unit sphere in higher dimensions here. We prove that the length of the inspecting curve is in $\Omega(d) \cap O(d^{3/2})$. It is a nice open question to find the precise asymptotics.